Question

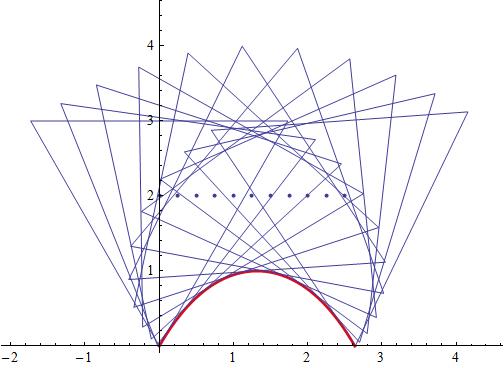
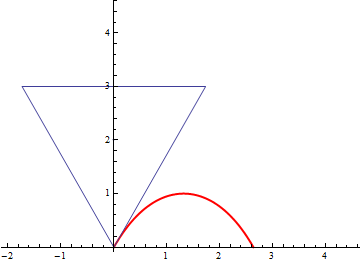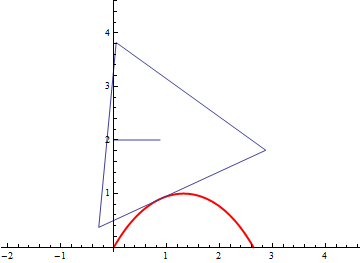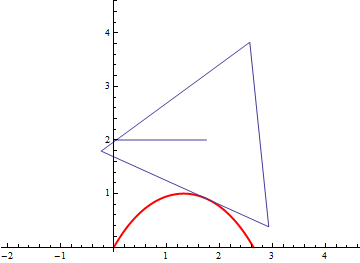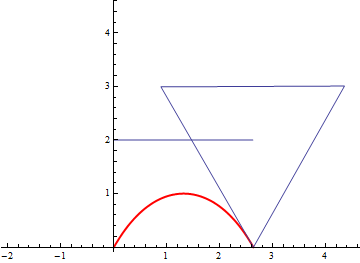
How does the profile of the ground have to be, to be able to drive with triangular wheels (equilateral) and without bumps?

Answer 1

To drive without bumps, the center of the "wheels" must remain at a constant height while driving. In other words, the distance from the center of the wheel to the point on the wheel touching the ground added to the distance from the point on the ground to some base level must be constant.

Noting that the former distance is maximal when a vertex is touching the ground, we consider a triangular wheel with side lengths `s` in such a position, and let the distance from the triangle's center to a vertex be our constant height. As the triangle is equilateral, we may calculate this as `s/sqrt(3)`. Next, consider a point on the side of the wheel as it rolls clockwise along the ground.

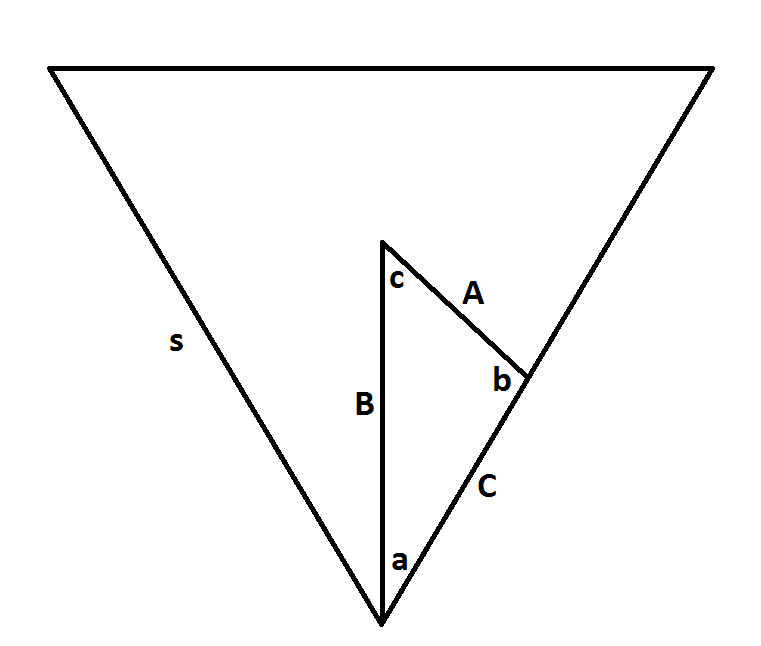
Referencing the above diagram, if the ground is touching point `b`, then for the center to remain at a constant height, we must have the sum of `A` and the ground's height be `s/sqrt(3)`. Letting `g` represent the height of the ground with `g=0` when a vertex is touching, this translates to `A+g = s/sqrt(3)`, or `g = s/sqrt(3)-A`.

We will now calculate `g` in terms of `c` as `c` goes from `0` to `(2pi)/3`, that is, as the wheel rolls from one vertex to the next.

Note that as the wheel is equilateral, its vertices each have an angle of `pi/3`, meaning `a = (pi/3)/2 = pi/6`. As `a+b+c = pi`, this gives `b = pi-pi/6-c = (5pi)/6-c`. Note additionally that `B = s/sqrt(3)`.

With these, we can now put `A` in terms of `c` by applying the law of sines (This does not apply at the single point where `b=pi/2`, however we will disregard that during the calculations and fill in that point explicitly after).

`A/sin(a) = B/sin(b)`

`=> A = (Bsin(a))/sin(b)`

`=(s/sqrt(3)sin(pi/6))/sin((5pi)/6-c)`

`=s/(2sqrt(3)sin((5pi)/6-c))`

Substituting this in for `A`, we can write `g` as

`g = s/sqrt(3)-s/(2sqrt(3)sin((5pi)/6-c))`

`=s/sqrt(3)(1-1/(2sin((5pi)/6-c)))`

Adding in the point where `b=pi/2` (i.e. where `c=pi/3`), the profile of the ground for the first third of a turn of the wheel is

`g = f(c)= {(s/sqrt(3)(1-1/(2sin((5pi)/6-c))), c in [0, pi/3)uu(pi/3,(2pi)/3]), (s/(2sqrt(3)), c = pi/3):}`

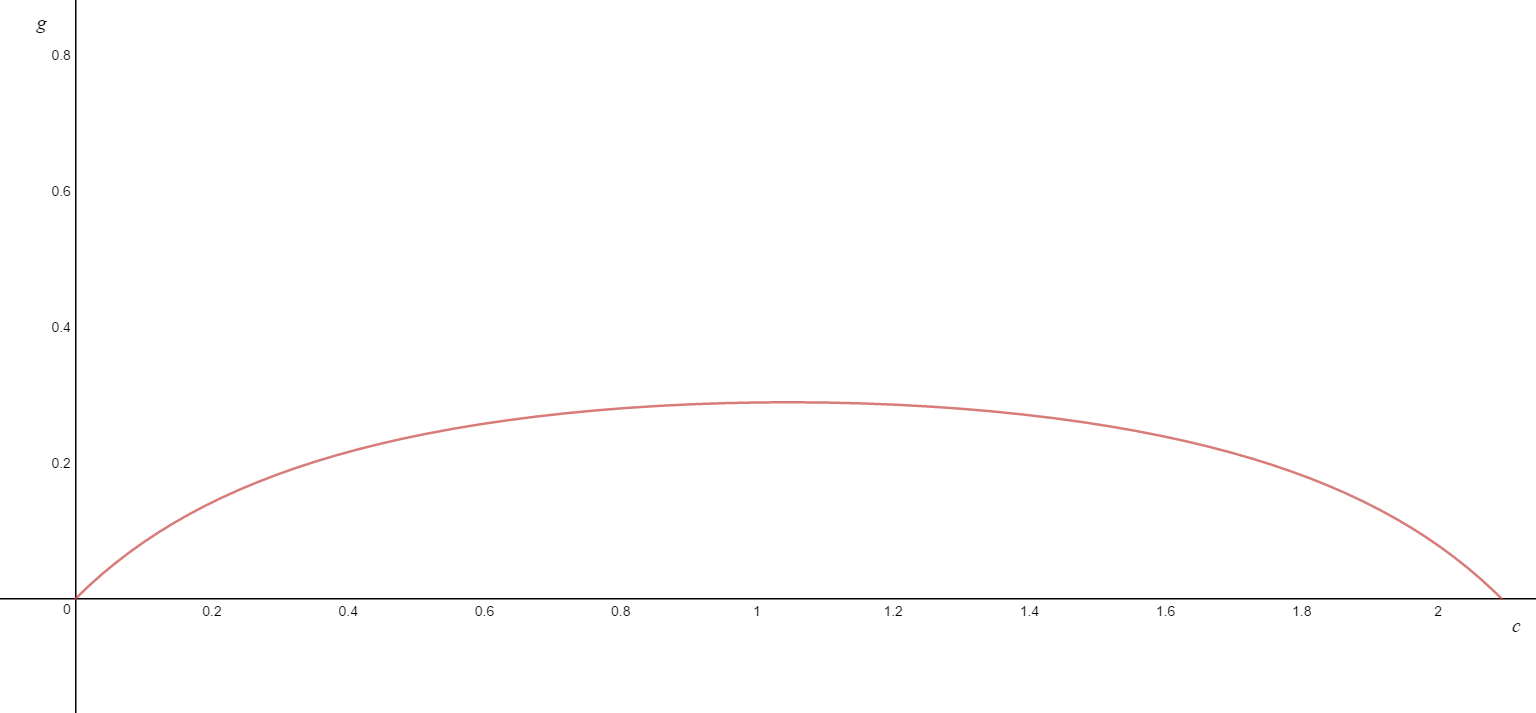
And, by symmetry, this pattern will repeat, giving us our full profile as

`g = f(c" mod" (2pi)/3)`

Answer 2

See below.

Explanation:

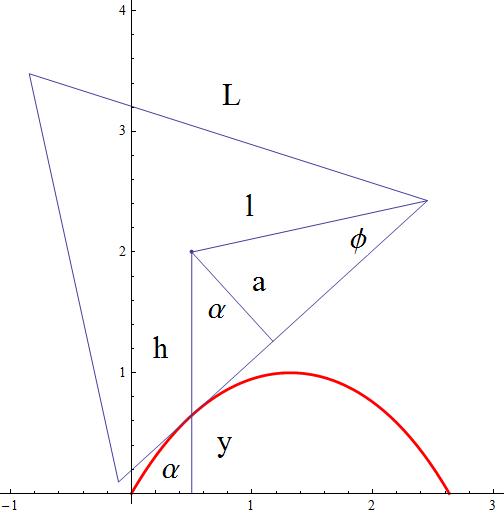
Calling `phi=pi/6` half the equilateral triangle angle's measure,

`a/l=sin(phi)`
`L/2=lcos(phi)`

then

`a=L/2 tan (phi)` The main line to proceed is the fact:

`a/cos (alpha) + y =h=2a`

because `tan(alpha)= (dy)/(dx)` so

`1/cos^2(alpha)=sec^2(alpha)=((h-y)/a)^2` but `1+tan^2(alpha)=sec^2(alpha)`

Substituting this last identity we get at

`((dy)/(dx))^2=((h-y)/a)^2-1` or

`(dy)/(dx)=sqrt(((h-y)/a)^2-1)`

This is the differential equation governing the contact line `y` equation.

Making now `z=(h-y)/a` we have

`(dz)/(dx)=1/asqrt(z^2-1)`

This is a separable differential equation. Solving we get

`z=1/2(cosh(x/a+C))`

solving now for `y`

`(h-y)/a=z` we obtain

`y=h-a cosh(x/a-C)`

`C` is determined by the initial conditions: `x=0->y=0`

and thus finally we obtain the contact line equation.

`y(x) = h-acosh(x/a-cosh^-1(h/a))`

All those rare "wheels" have catenary support.

The period of this catenary is found by solving for `x`

`y(0)=h-acosh(T/a-cosh^-1(h/a))=0` finding

`T=2a cosh^-1(h/a)`

As a verification, making `a=1, h=2a=2` we obtain the graphics attached.