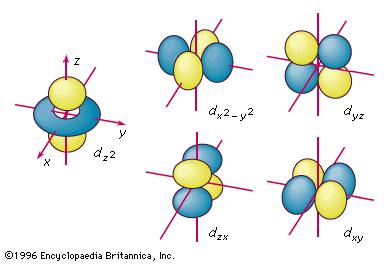
How many d orbitals can there be in one energy level?

1 Answer
Truong-Son N.
Jul 20, 2016

This depends on the number of magnetic quantum numbers #m_l# that correspond to a single angular momentum quantum number #l#.

  • #n# is the principal quantum number (the energy level) going as #1, 2, 3, . . . , N#, and #N# is a large integer. For one energy level, #n# is only one number at a time.
  • #l# is the angular momentum quantum number, and it goes as #0,1,2, . . . , n-1#. For one subshell, #l# is only one number at a time, and #l = 0,1,2,3,4 . . . # corresponds to the #s,p,d,f,g, . . . # subshells. However, there can be more than one #l# for the same energy level.
  • #m_l# is the magnetic quantum number, and takes on all numbers in the set #{-l, -l + 1, . . . , 0, . . . , +l - 1, +l}#. It corresponds to how many orbitals are in a subshell.

For an energy level to validly have #d# orbitals, #n >= 3#. Any smaller #n#, and the number of #d# orbitals is #0#.

For any #n#, #l <= (n-1)# is allowed, and for #d# orbitals, #l = 2# (of course, #2 = 3 - 1#, so that's why #n >= 3# for #d# orbitals). Therefore, what we have for #m_l# is:

#color(blue)(m_l = {-2,-1,0,+1,+2})#

So, there are #2l+1 = \mathbf(5)# different (but degenerate, same in energy) #d# atomic orbitals in the same #nd# subshell.

Example

#3d_(xy)#, #3d_(xz)#, #3d_(yz)#, #3d_(x^2-y^2)#, #3d_(z^2)#:

https://media1.britannica.com/

Related questions
See all questions in s,p,d,f Orbitals
Impact of this question
12294 views around the world
You can reuse this answer
Creative Commons License