How many #"g"# of water are required to be mixed with #"11.75 g"# of #HgCl# in order to make a #"0.01 m"# solution?
1 Answer
4,980 g
Explanation:
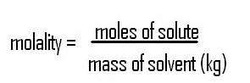
We know the molality (m), but not the number of moles of solute. The mass of solute can be converted into moles using the molar mass of HgCl (236.04 g/mol) as a conversion factor:
Since the moles of solute and molality are known, we can rearrange the equation to solve for mass of solvent :
Lastly, the mass of solvent has to be converted from kg to g using the following conversion factor:

Therefore,
4,980 g

