Question

How many orbitals are in each sublevel?

Answer 1

That depends on the subshell.

Explanation:

Electrons that surround an atom's nucleus are distributed on specific energy levels, or shells.

Each shell is made up of a different number of subshells. More specifically, the number of subshells a shell can have increases as you move away from the nucleus.

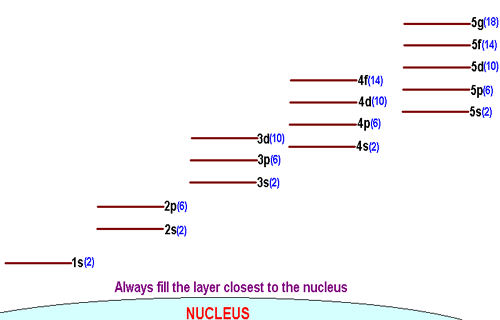
You can use quantum numbers to illustrate this point.

The principal quantum number, `n`, gives you the energy level, or shell.

Now, the number of subshells is given by the angular momentum quantum number, `l`, which can take values from `0` to `n-1`.

This means that you will have

• `n = 1 implies l = 0 ->` the first shell only has one subshell, s
• `n = 2 implies l = 0, 1 ->` the second shell has two subshells: s and p
• `n = 3 implies l = 0, 1, 2 ->` the third shell has three subshells, sp, p, and d
  `vdots`

and so on.

The number of orbitals each subshell contains is given by the magnetic quantum number, `m_l`, which takes values from `-l` to `l`.

So, for example, how many orbitals would you say the 2p-subshell has?

Well, the 2p-subshell has `l = 1`, which means that `m_l` can be

`m_l = {-1, 0, 1} ->` the 2p-subshell contains 3 orbitals.

How about the 3d-subshell?

For the 3d-subshell, you know that `l = 2`. This means that `m_l` can be

`m_l = {-2, -1, 0, 1, 2} ->` the 3d-subshell contains 5 orbitals.

So, as a conclusion, you get th number of orbitals per subshell from the principal quantum number, `n`, which in turn gives you the value of the angular momentum quantum number, `l`.

The magnetic quantum number, the ones that tells you exactly how many orbitals you get per subshell, will always take values from `-l` to `l`, so if you know `l`, you automatically know `m_l`.