Question

How to calculate the potential energy of an electron in the `"nth"` shell (also take example `"n=3"` shell) of a copper atom using the Hartree Fock Theory? Also calculate its kinetic energy

Answer 1

You can't calculate the kinetic energy of an electron that hasn't left the atom. So we could only calculate the orbital potential energy.

---

DISCLAIMER: COMPLICATED ANSWER!

Since copper is not that heavy, we don't have to worry too much about scalar relativistic effects or spin-orbit coupling. In fact, its ground electronic state is a `""^2 S_"1/2"`, with no low-lying excited states to include in a more multi-referenced level of theory like MCSCF or CCSD(T).

The ground-state electron configuration would be:

`[Ar] 3d^10 4s^1`

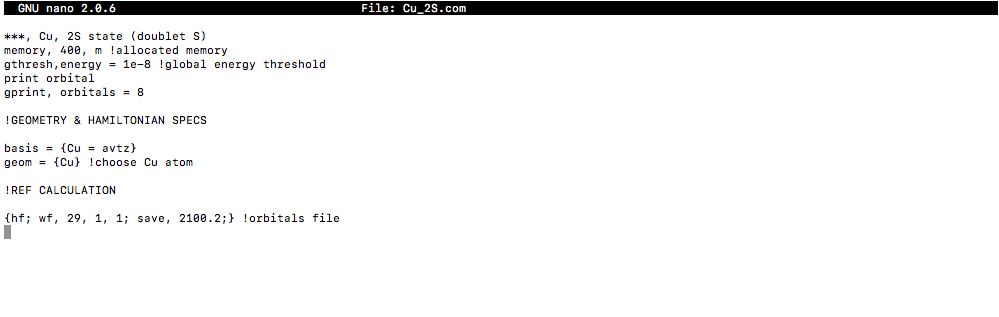
INPUT FILE SETUP

At the Hartree-Fock level of theory (a single-reference method), we assume a single configuration with doubly-occupied core and `3d` valence orbitals, and a singly-occupied `4s` valence orbital. We don't expect good agreement with experiment with this level of theory...

MolPro, Psi4, and other computational software could do this, but I have MolPro with me right now. A basic input for copper atom would look like this:

[

Here,

• `400` megawords are used for the memory (32 bits per word on a 32-bit machine, etc).
• Only the Abelian point groups are used, and by default for atoms, `bb(D_(2h))` is used.
• copper is using an augmented correlation-consistent polarized valence triple zeta basis set, with basic atomic geometry specified.
• The atom has `29` electrons, the unpaired electron is of `A_g` symmetry (symmetry 1), and has twice the total spin, `2 xx S`, of `1`, as specified by the wave function card:

`"wf, 29, 1, 1"`

VERIFYING THE ORBITAL OCCUPATION

The orbitals in the basis set are being printed in order by energy within each irreducible representation of the `D_(2h)` point group, whose irreducible representations are listed as `A_g`, `B_(3u)`, `B_(2u)`, `B_(1g)`, `B_(1u)`, `B_(2g)`, `B_(3g)`, `A_u`.

So, orbital `6.1` is the sixth orbital (starting from the lowest energy) of `A_g` symmetry, orbital `2.5` is the second orbital of `B_(1u)` symmetry, etc.

We expect the orbital occupation is ordered as follows:

`ul(A_g" "B_(3u)" "B_(2u)" "B_(1g)" "B_(1u)" "B_(2g)" "B_(3g)" "A_u)`
`1s" "2p_x" "2p_y" "3d_(xy)" "2p_z" "3d_(xz)" "3d_(yz)" "-`
`2s" "3p_x" "3p_y" "" "" "color(white)(.)3p_z`
`3s" "`
`3d_z^2" "`
`3d_(x^2 - y^2)`
`color(red)(4s)" "`

where red indicates the singly-occupied orbital with one spin-up electron.

MolPro believes it to be:

[

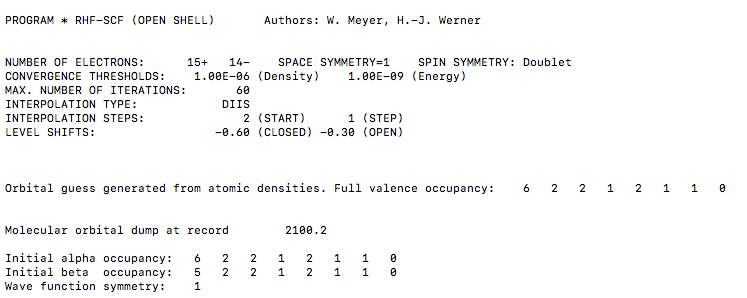
The orbital occupation looks correct on the first go, but in practice, you should specify the occ and closed cards anyway. It should be an occupied configuration of:

`(A_g, B_(3u), B_(2u), B_(1g), B_(1u), B_(2g), B_(3g), A_u) = (6, 2, 2, 1, 2, 1, 1, 0)`, specified by

`"occ, 6, 2, 2, 1, 2, 1, 1, 0"` within the brackets for the HF command.

and a closed-shell (doubly-occupied) configuration of:

`(A_g, B_(3u), B_(2u), B_(1g), B_(1u), B_(2g), B_(3g), A_u) = (5, 2, 2, 1, 2, 1, 1, 0)`, specified by

`"closed, 5, 2, 2, 1, 2, 1, 1, 0"` within the brackets for the HF command

indicating one spin-up electron in the `4s` orbital (since it is the sixth orbital in symmetry 1).

ORBITAL ENERGIES (BE CRITICAL!)

The orbital output was:

[

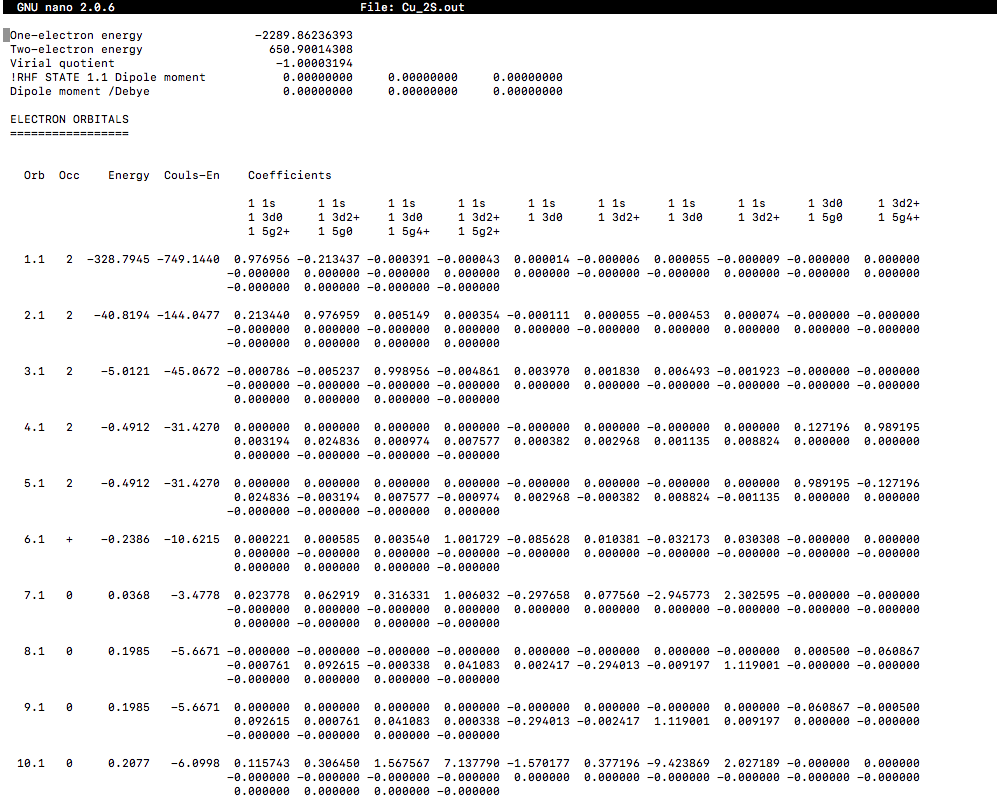
The default energies listed are in Hartrees, so you'll have to convert to `"eV"`s if you want them in `"eV"`s. There are `"27.2114 eV"`s per Hartree.

Apparently, the HOMO, the `4s` (orbital `6.1`), was (poorly) calculated to have an energy of `-"6.49 eV"`, which is too high in energy by about `"2 eV"`...

The `3d`, orbital `5.1` (orbital five of symmetry `A_g`), lists an energy of `bb(-"13.37 eV")`, which is quite close to the actual `-"13.47 eV"` here.

The `3p` orbitals are the last orbitals in symmetry 2, 3, and 5, so they are orbitals `2.2, 2.3, 2.5`. These have calculated energies of `-"90.48 eV"`, which is quite low and certainly core-like. I am not at all sure if these `3p` energies are correct, but who really cares about the core orbitals in a light atom like this (especially since the `3d` subshell is full)?

For a basic calculation at a low level of theory, this isn't that bad...