There is no orbital hybridization in either of these diatomic compounds.
Note that in linear diatomic molecules, the #p_z# orbital always points along the internuclear axis, so it has to contribute to one of the #sigma# bonds.
I've drawn the overlaps below in the MO diagrams.
BROMINE BONDING (HOMONUCLEAR DIATOMIC)
For #"Br"_2#, it is the simpler of the two examples. It is a homonuclear diatomic, so all of its orbitals have a compatible partner: #4p_x# with #4p_x#, #4p_y# with #4p_y#, etc.
In this case, since there are only two atoms, they use their highest energy compatible orbitals to #sigma# bond on the internuclear axis. The energy of the #4s# atomic orbital is #-"24.37 eV"#, and the #4p# atomic orbitals are #-"12.49 eV"# in energy (Inorganic Chemistry, Miessler et al., Table 5.2).
Each bromine would donate one #\mathbf(4p_z)# electron to form a #sigma#-bonding orbital.
As a result, there is no orbital hybridization here.
Here is the MO diagram below (I had to draw it myself since I couldn't find one online; the #pi_(4px)# and #pi_(4py)# orbitals---the #1b_(3u)# and #1b_(2u)#---are very close in energy to the #sigma_(4pz)#, the #1b_(1u)#):
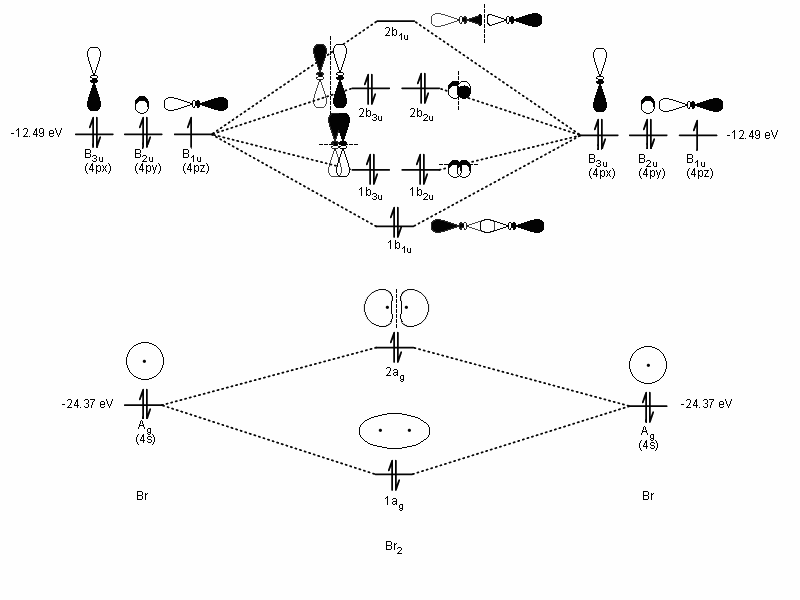
Granted, that is not #"Br"_2#'s highest-occupied molecular orbital (that would be the #pi_(4px)^"*"# and #pi_(4py)^"*"#---the #1b_(3u)# and #1b_(2u)#), but since both the bonding and antibonding #pi# molecular orbitals are occupied, it is the #sigma_(4p_z)# (#1b_(1u)#) that participates in the #sigma# bond.
You should notice that the #1b_(1u)# orbital is the #sigma_(4pz)# bonding orbital, but the #2b_(1u)#---the #sigma_(4pz)^"*"# antibonding orbital---has no electrons, so it doesn't contribute to the #sigma# bond. If it did, #"Br"_2# would not exist.
Therefore, the #sigma_(4pz)# indeed is the molecular orbital that represents the single bond on #"Br"_2#.
NO#""^(\mathbf(+))# BONDING (HETERONUCLEAR DIATOMIC)
#"NO"^(+)#, on the other hand, is a heteronuclear diatomic. Since it is also diatomic, it also does not need to hybridize.
All of nitrogen's orbitals are compatible with oxygen's orbitals in energy (and in symmetry, but that is less crucial to our understanding for General Chemistry level education).
The MO diagram for neutral #"NO"# is as follows (Inorganic Chemistry, Miessler et al., Ch. 5, Answer Key):
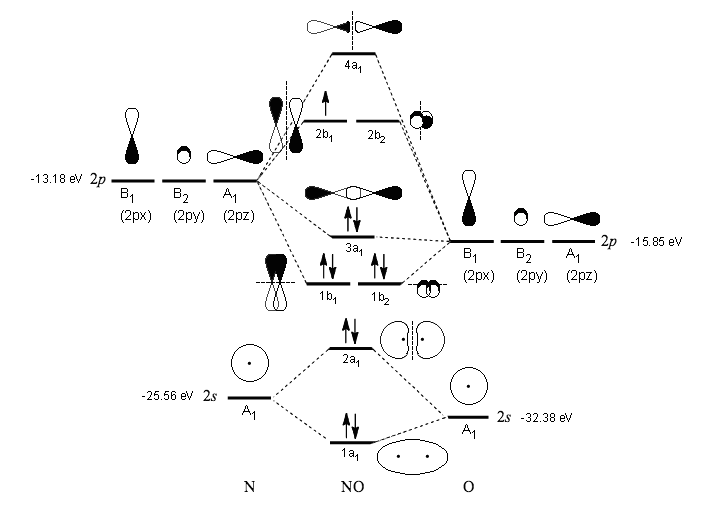
(I superimposed some orbital depictions on the original diagram, and added symmetries and energies.)
If we consider #"NO"^(+)#, we remove the electron from the highest-occupied molecular orbital, so we take out the one from the #pi_(2px)^"*"# antibonding orbital (#2b_1#) to form #"NO"^(+)#.
At this point, its bonds have increased in strength. The bond order changed from:
#(8 - 3)/2 = 2.5#
to:
#(8 - 2)/2 = 3#
So we know it has a triple bond. That means it needs three orbitals contributed from each atom.
There are two electrons in the #sigma_(2pz)# molecular orbital (#3a_1#), and there are two electrons each in the #pi_(2px)# (#1b_1#) and #pi_(2py)# (#1b_2#) molecular orbitals.
#"NO"^(+)# therefore uses two #2p_x# atomic orbitals, two #2p_y# atomic orbitals, and two #2p_z# atomic orbitals to bond.
As a result, there is no orbital hybridization here.
Each #sigma#-bonding pair contributes to a #sigma# bond, and each #pi#-bonding pair contributes to a #pi# bond. That accounts for the triple bond: one #sigma# and two #pi# bonds.



