How do you find the volume of the solid formed by rotating the region enclosed by ?

about the x-axis.

about the x-axis.
3 Answers
Explanation:
We'll use a method call the disk method to do this.
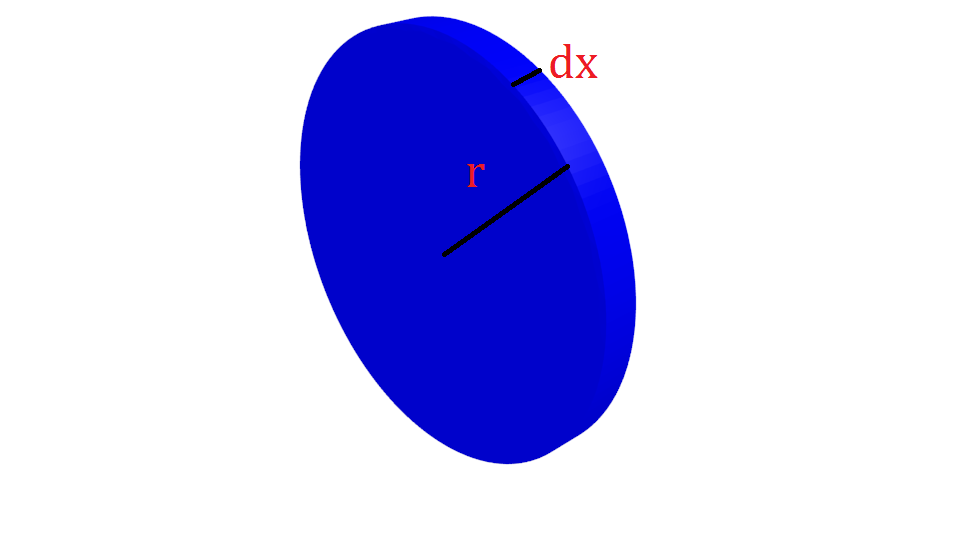
Take a look at the above picture. Pretend it's an infinitely small cylindrical disk, with radius
We know volume of a cylinder is given by:
And we know that the radius of each cylinder is the value of
Integrating both sides to find total volume, for
But
Expanding the
And using the sum rule:
Finally, evaluating these one by one:
Awesome Ken...
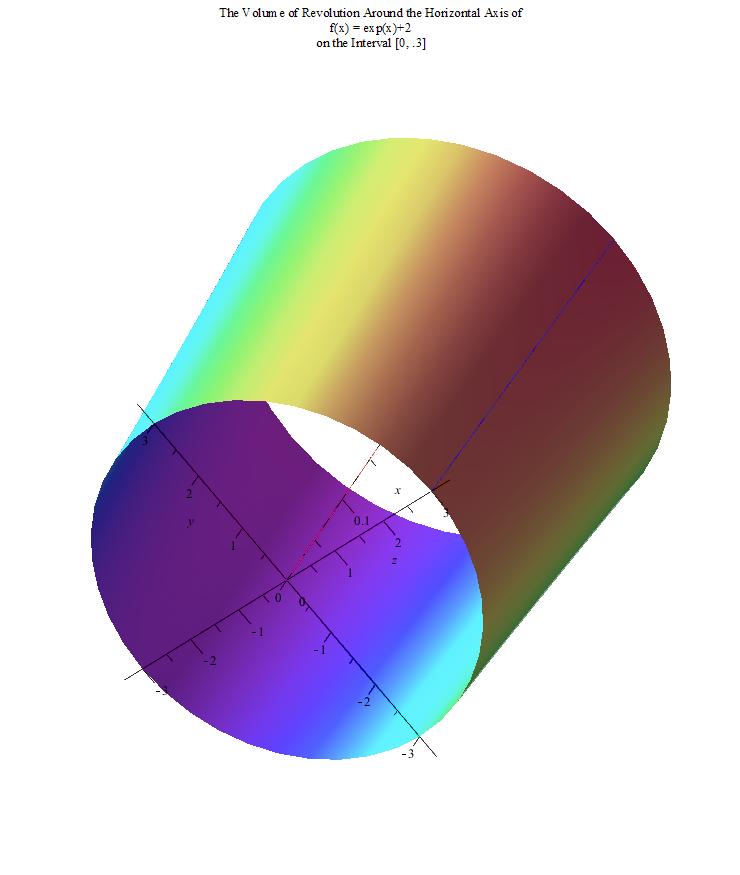
Here is a Maple rendering of the rotation!
By the way, you have the coolest name in the world.
0.9117
Explanation:



