How to solve the system of equations 2x-y=-1 and 3x+2y=-5 by graphing?
1 Answer
From the graphs, we get point of intersection at 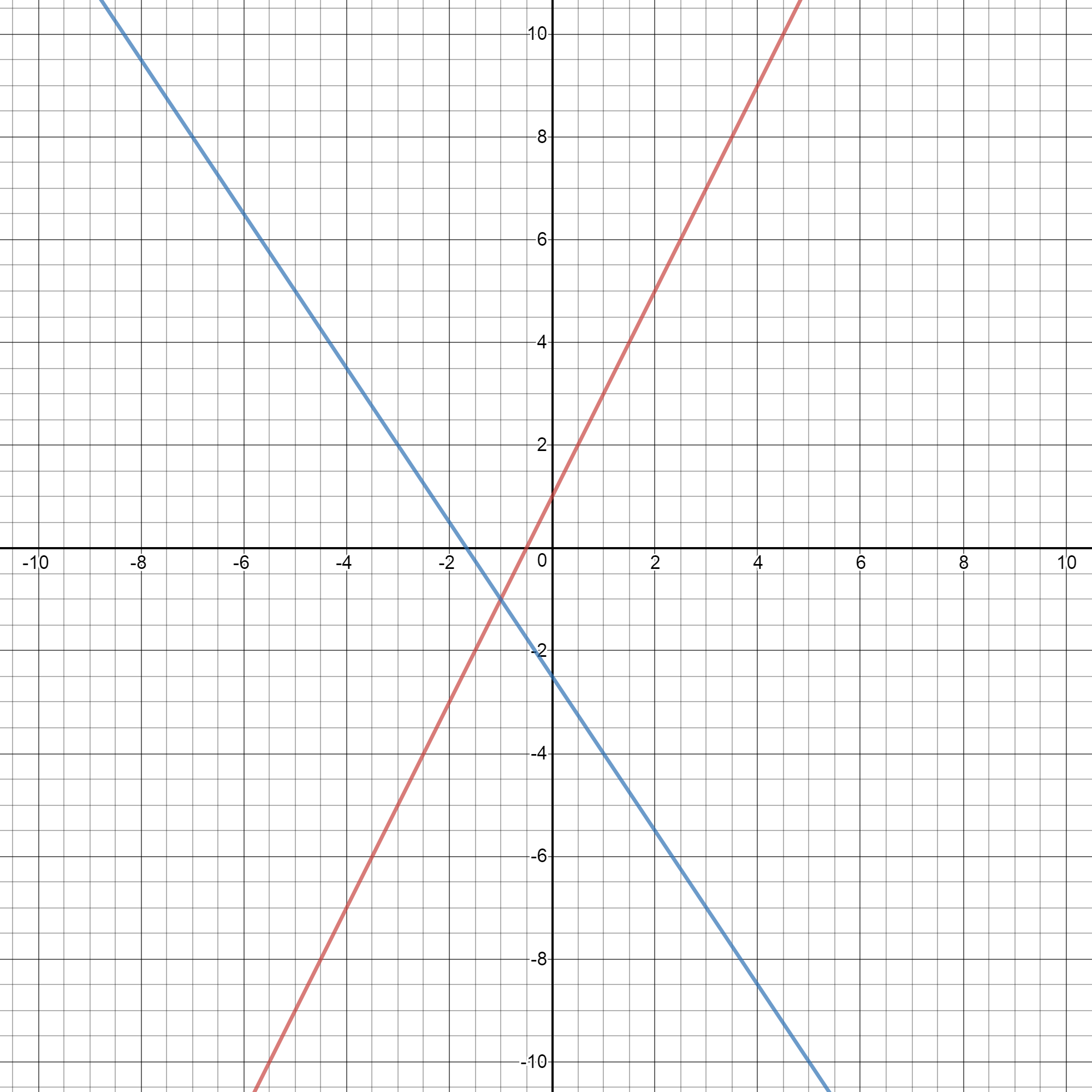
Explanation:
The intercept of two linear graphs is the solution for
Lets take the first equation:
Find the
Lets take the second equation:
Find the
**Now plot the two linear graphs and from the graph, the intersection of these tow linear graphs are the value of
From the graphs, we get point of intersection at

