How would I find the area of a 45-45-90 triangle with one side of length 73?

Question

2906 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-11-25T03:27:54

#AB = 73 sqrt2, BC = AC = 73#

enter image source here

Now i hope you are aware of the Pythagoras Theorem which states;

#AB^2 = BC^2 + AC^2#

Additionally
enter image source here

This is the definition of a Pythagorean triplet where m>n

Now notice BC = AC in the above image

For this scenario we have special formula;

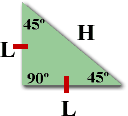
enter image source here

#H = Lsqrt2#

So this is a nice template for this type of a triangle;

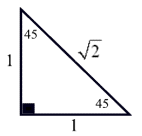
enter image source here

For the side provided to be the hypotenuse it has to be a multiple of #sqrt2# which clearly it isn't;

So we can make out first assumption

#BC = AC = 73#

Now its just substitution;

#73^2 + 73^2 = x^2#

#sqrt(73^2 + 73^2) = x#

#x = sqrt(2*73^2)#

#=>AB = 73 sqrt2#