How would you compare the three types of bonds based on what happens to the valence electrons of the atoms?
1 Answer
So we compare
Explanation:
The modern covalent bond is conceived to be a region of high electron density between 2 positively charged atomic nuclei such that internuclear repulsion (on the basis of the electrostatic repulsion of like charges) is NEGATED, and a net attractive force results. Covalent bonds are thus highly directional, and if we map electron density between the bound nuclei, there is maximum density along the direction of the bond.
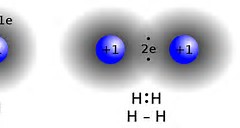
I am not entirely happy with this diagram, as it does not reflect the the maximized electron density between the hydrogen atoms.....Here is another attempt:
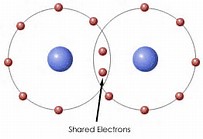
The point I wish to illustrate is that there is high electron density BETWEEN the nuclei.
On the other hand,
Of course, cations, and anions, are electrostatically repelled by every cation, and anion is the lattice, but if you sum up attractive versus repulsive interactions across the lattice, which can certainly be done quantitatively, a net attractive force operates over the entire lattice. And thus ionic solids have high melting and boiling points, which reflects their molecularity (which is ZERO), and tend to be brittle solids, while having very high melting points. Solutions of ionic solids, when they can be dissolved in a solvent, thus also exhibit electrical conductivity.
And lastly we come to
And in this way the properties of metals, covalent solids, molecular gases and liquids can be rationalized on the basis of their peculiar electronic structure.

