Question

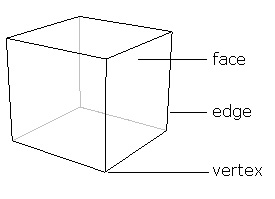
I have 6 faces, 8 vertices, and 12 edges. Which figure am l?

Answer 1

It is a cuboid or quadrilaterally-faced hexahedron.

Explanation:

There is no unique formula for getting the figure. However, according to Euler's Polyhedral Formula, in a convex polyhedra, if `V` is the number of vertices, `F` is number of faces and `E` is number of edges than `V-E+F=2`.

It is apparent that with `6` faces, `8` vertices, and `12` edges, then `8-12+6=2`, hence it is a valid polyhedra.

However, it is evident that the figure is a cuboid or quadrilaterally-faced hexahedron, as it too has `6` faces, `8` vertices, and `12` edges.