Question

If a `1 kg` object moving at `3 m/s` slows down to a halt after moving `8 m`, what is the friction coefficient of the surface that the object was moving over?

Answer 1

`mu_k~~0.0573`

Explanation:

It's very useful to organize the given information in a table to be able to identify the formulas that would be efficient to use.

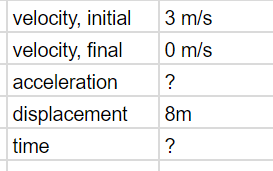
The acceleration is the variable we need to solve for to acquire the net force on the object. The formula, `v^2=v_o^2+2ad` where `v` is the final velocity, `v_o` is the initial velocity, `a` is the acceleration, and `d` is the displacement, best allows us to solve for the net acceleration. With the mass (1 kg), we can calculate the net force.

`v^2=v_o^2+2ad`
`a=(v^2-v_o^2)/(2d)`
`a=(0^2-3^2)/(2*8)`
`a=-9/16 m/s^2`
`SigmaF=m*bar a`
`SigmaF=-9/16 N`

The acceleration that slows this object down comes from the frictional force from the surface that the object is sliding on which is defined as `F_f=F_n*mu_k`. Assuming the object is on a horizontal surface, the `F_n=mg` or the gravitational force on the object.

( In the following picture, the direction of movement it to the right, the forces interacting on the y-axis, normal force and gravitational force, are of equal magnitude, and the frictional force is opposite to the motion.)

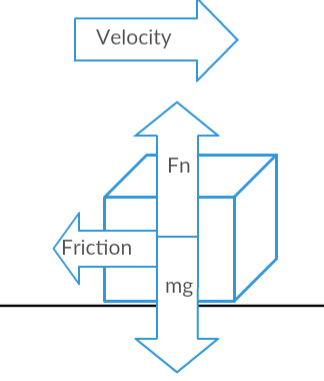
The net force is equal to the frictional force only since the upward normal force cancels out the downward gravitational force therefore, `SigmaF=F_f`. By substituting `F_f` with its definition, we get the equation
`SigmaF=F_n*mu_k`
Where we can then substitute `F_n` for `mg`
`SigmaF=mg*mu_k`
`mu_k=(SigmaF)/(mg)`
`mu_k=(-9/16N)/(-9.81N)~~0.0573`

Answer 2

`mu_k = 0.056`

Explanation:

Well, the force of friction `F_f` is defined as the following...

`F_f = mu_k N`

And the normal is given by...

`N = mg`

`N = (1)(9.81)`

`N = 9.81N`

So now, we need to calculate an acceleration to get the force of friction. We are assuming in this question that `F_(drive) = F_f` because all the energy that the mass possess is lost to friction.

`v^2=u^2-2as`

`0^2 = 3^2 -2(8)a`

`0 = 9-16a`

`a = (-9)/(16)`

`a= -0.5625 ms^-2`

`F_f=ma`

`F_f=(1)abs(-0.5625)`

`F_f=0.5625N`

`mu_k = F_f/N`

`mu_k = 0.5625/9.81`

`mu_k = 0.057`