Question

If an object is moving at `15 m/s` over a surface with a kinetic friction coefficient of `u_k=25 /g`, how far will the object continue to move?

Answer 1

The object will travel `4.5m` before stopping.

Explanation:

Given the kinetic friction coefficient of `mu_k=25/g`, I have to assume that `g` is either some variable which has no relation to the free-fall acceleration, `g`, or it is supposed to represent the magnitude of `g`, `9.8` (no units). If you include the units of `g`, the calculation will not work out as you will be left with units of `m^2/s^2` rather than `m^2` for distance traveled. In addition, coefficients of friction have no units, so a value of `mu_k=25/(9.8m/s^2)` would not be valid.

My solution uses the work-energy theorem.

`W=DeltaE_(system)`

`=>W_(n e t)=DeltaK`

We can use that the net work done on the object is equal to the change in kinetic energy to calculate the distance traveled by the object. If friction were not involved, energy would be conserved, i.e. there would be no change in energy of the system (`DeltaE=0`). Obviously there is a change of energy, because the object slows down and eventually comes to rest, indicating that it is losing energy as it moves across the surface. When it comes to rest, it has lost all of the energy it originally possessed. We can assume that loss in energy is due to friction, where kinetic energy is lost to heat energy produced by friction.

A force diagram for this situation would look something like this:

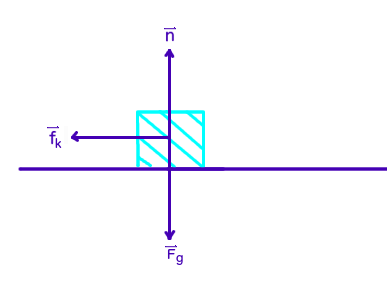
Where `vecn` is the normal force, `vecf_k` is the force of kinetic friction, and `vecF_g` is the force of gravity. Note that I have defined motion to the right as positive.

It is important to realize that only forces which act parallel to the motion of the object do work on the object. This means that the force of friction is the only force present in this situation which does work. The equation for work is given by `W=vecF*Deltar*cos(theta)`, where `vecF` is the applied force, `Deltar` is the distance over which the force is applied, and `theta` is the angle between the force and displacement vectors. When the force is perpendicular to the motion, `theta=0^o` or `theta=270^o`. Both produce a value of `0` by the cosine function, resulting in `W=0`.

The force of kinetic friction works opposite the direction of motion to slow the object down, so `theta=180^o` and `cos(180^o)=-1`, giving that the work done by friction is negative. We would expect this to be the case, as friction works against the motion. Parallel forces acting in the same direction of motion give `theta=0^o`, and `cos(0^o)=1`, reducing the work equation to the more familiar `W=vecF*Deltar` or `W=Fd`.

The object is moving initially, but we want to know how far it travels, or how far it moves before it stops. Therefore, the object is at rest finally, or has `vecv_f=0`. From the work-energy equation given above, we are concerned with the change in kinetic energy, `DeltaK`. Kinetic energy is given by `K=1/2mv^2`, and the change in kinetic energy is therefore given by

`DeltaK=1/2m(v_f)^2-1/2m(v_i)^2`

We determined that the object should be at rest finally and therefore have no final velocity, giving:

`DeltaK=-1/2m(v_i)^2`

Back to our work-energy equation:

`W=DeltaK=-1/2m(v_i)^2`

And we determined that the only work done is by friction:

`=>W_F=-1/2m(v_i)^2`

From the above equation for work,

`W_f=-vecf_k*Deltar`

We know that the force of kinetic friction is given by:

`vecf_k=mu_kvecn`

From a vertical sum of forces statement for the object:

`sumvecF_y=vecn-vecF_g=cancel(mveca)=0`

`=>vecn=vecF_g`

`=>vecn=mg`

So we have now that:

`vecf_k=mu_kmg`

Back to our work-energy equation:

`-mu_kmg*Deltar=-1/2m(v_i)^2`

Rearrange to solve for `Deltar`:

`Deltar=(cancel-1/2cancelm(v_i)^2)/(cancel-mu_kcancelmg)`

Cancel negative signs and mass

`Deltar=(1/2(v_i)^2)/(mu_kg)`

Given that `v_i=15m/s` and `mu_k=25/g=25/9.8`:

`Deltar=(1/2(15m/s)^2)/(25/cancel9.8*cancel9.8m/s^2)`

`Deltar=(225/2m^2/s^2)/(25m/s^2)`

`Deltar=(225/2m^(cancel2)/cancels^2)*(cancels^2/(25cancelm))`

`Deltar=225/50m=4.5m`

---

Because the answer works out fairly well, I assume that is what is meant by `mu_k=25/g`. If `g` is just a variable, you would end up with:

`Deltar=(225/2m^2/s^2)/(25/g*9.8m/s^2)`

`Deltar=(225/2m^2/s^2)/(245/gm/s^2`

`Deltar=(225/2m^(cancel2)/cancels^2)*(gcancels^2)/(245cancelm)`

`Deltar=(225g)/(490)m`

`Deltar=(45g)/98m`

Where `g` is some variable.