If sides A and B of a triangle have lengths of 2 and 4 respectively, and the angle between them is #(pi)/4#, then what is the area of the triangle?
1 Answer
Explanation:
One way to do this is strictly geometrical.
Consider the square containing the given triangle with the side of length
We would have the structure below:
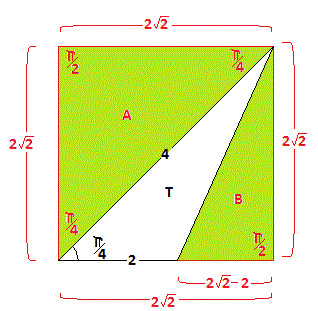
We are asked for the area of
and it is clearly
With a diagonal of length
Therefore the area of the
The area of
The area of
The area of
