If sides A and B of a triangle have lengths of 5 and 7 respectively, and the angle between them is #(5pi)/12#, then what is the area of the triangle?
1 Answer
Oct 2, 2017
Explanation:
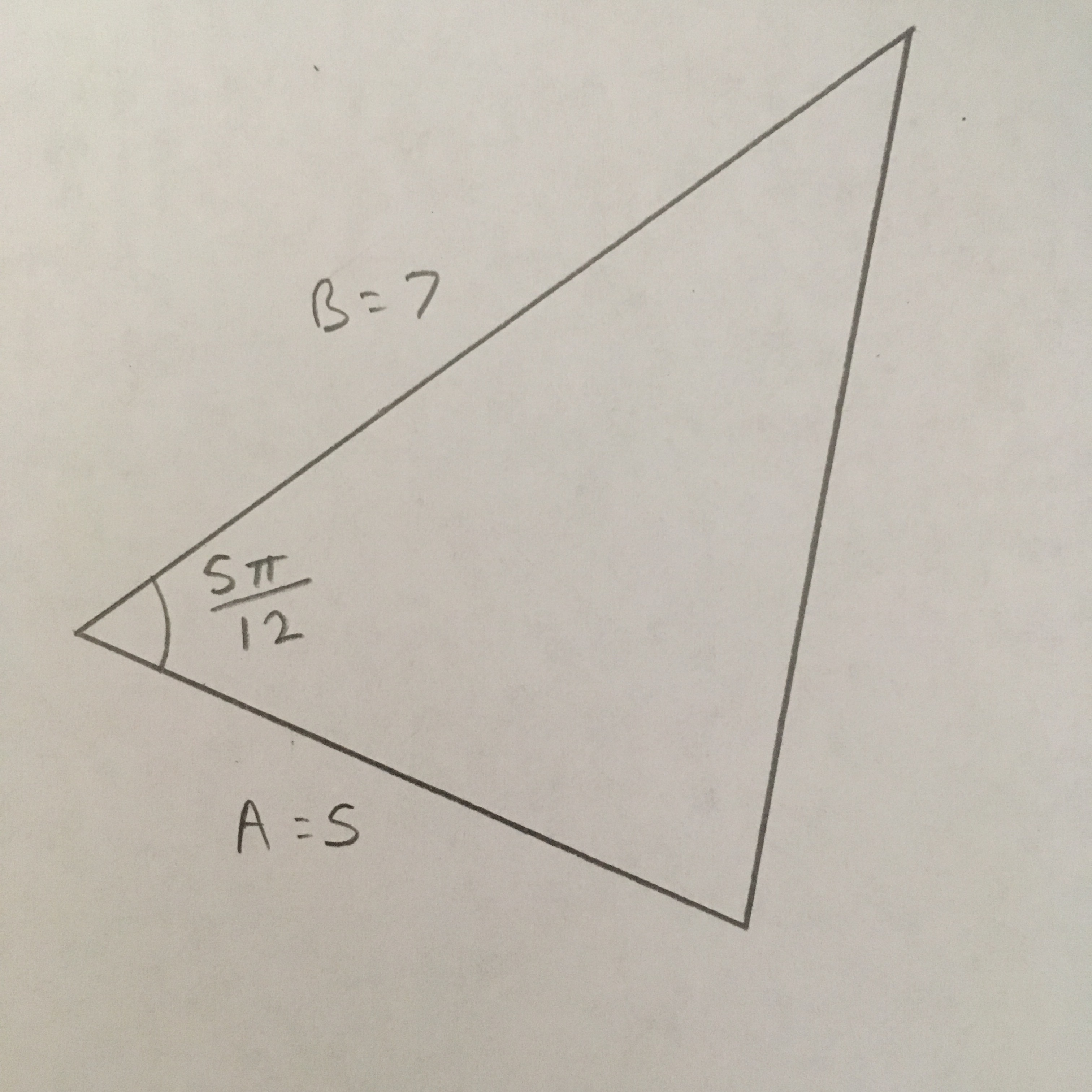
Using the formula
where

