Question

If sides A and B of a triangle have lengths of 9 and 12 respectively, and the angle between them is `(pi)/3`, then what is the area of the triangle?

Answer 1

`27sqrt(3)`

Explanation:

Taking a look at the triangle, we have something like the following:

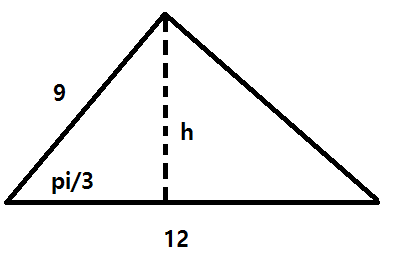
From the right triangle containing the angle `pi/3` we have

`sin(pi/3) = h/9 => h = 9sin(pi/3) = (9sqrt(3))/2`

Then, applying the area formula `A = 1/2bh`

`"area" = 1/2(12)((9sqrt(3))/2) = 27sqrt(3)`