Question

If the last orbital of an element has been incompletely filled, half filled and full filled which one is the most stable and which is least stable? Write the sequence.

Answer 1

It depends on the atom. For half-filled subshells, there is no special absolute rule that half-filled subshells are more stable than not-half-filled. That is not a rule atoms follow, because atoms know nothing of the rules we come up with.

Try reading this book from pg. 27 to the middle of pg. 29, and then going through example 2.2 for supplementary info regarding exchange energy and coulombic repulsion energy.

In a completely general case, taking `3d` and `4s` orbitals in these five example isolated configurations (assuming that there are no other orbitals nearby in energy):

`" "" "" "" "" "" "(1a)`

`ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(color(white)(uarr darr))`

`" "" "" "" "" "" "`

`" "" "" "" "" "" "(1b)`

`ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(darr color(white)(darr))`

• `E(1b) < E(1a)` because it has more electrons in degenerate orbitals (of the same energy). Each electron added in the absence of electron-electron interaction tends to decrease the energy of the atom.

This is because it takes energy input to remove an electron, so adding an electron ideally would release energy. That is why electron affinities tend to be negative.

`" "" "" "" "" "" "(2)`

`ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))" "ul(uarr color(white)(darr))`

• `E(2) < E(1b)` because now all these electrons have the same spin, increasing the magnitude of the stabilizing quantum-mechanical exchange energy (which is negative) between electrons of the same spin.

Consequently, we probably have `E(2) < E(1a) < E(1b)`. But again, this does not consider the presence of other orbitals nearby.

`(3a)" "" "" "" "" "(3b)`

`ul(uarr color(white)(darr))" "" "" "" "ul(uarr darr)`

• `(3b)` is not necessarily more stable for the atom overall than `(3a)`, because we've added an electron to fill all available `4s` quantum states (stabilizing), but also added coulombic electron repulsion (destabilizing).

That means we've included two counteracting effects, and more info is needed.

---

DEBUNKING THE HALF-FILLED SUBSHELL MYTH

We assume the "last orbitals" to be filled (as written in the question) for the first-row transition metals are the `(n-1)d` (but really, it tends to be the `ns`...).

Take chromium and tungsten for examples having orbital subshells we expect to be half-filled on the basis of periodicity:

`"Cr": [Ar] 3d^color(blue)(5) 4s^color(blue)(1)` (matches expectation, labeled an 'exception')

`"W": [Xe] 5d^color(red)(4) 6s^color(red)(2)` (does not match 'exception' expectation at first glance)

Since chromium and tungsten are in the same periodic table column, we would expect their electron configurations to be similar, but they are not. That is a sign that...

...having a half-filled subshell is not always the most stable configuration.

This book presents a more complete explanation on pg. 34 - 35. Consider the following diagram:

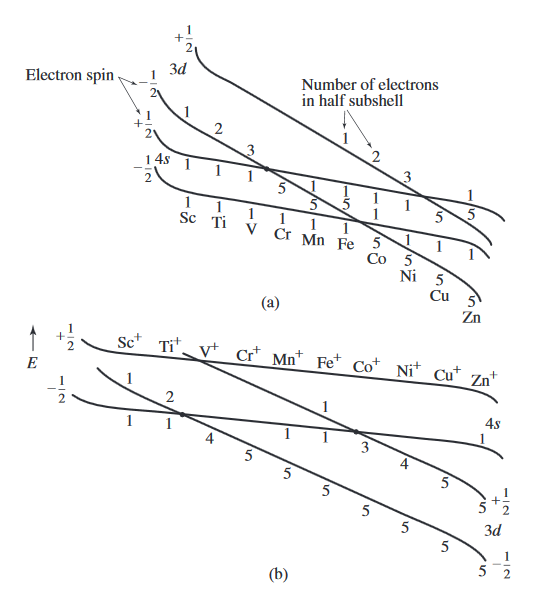
The book uses the convention that the first electron added has `m_s = -1/2` (spin-down).

Here, notice the shift in the `4s` electron energies from `(b)` to `(a)`. Figure `(a)` shows the `3d^5 4s^1` configuration of `"Cr"`, while figure `(b)` shows the `3d^5 4s^0` configuration of `"Cr"^(+)`.

For `"Cr"`, the `4s` electron happens to become lower in energy than the `3d` electrons after adding the last electron into the `4s` orbital of `"Cr"^(+)`, so it is more favorable to END UP having the `3d` orbitals half-filled.

This does not depend on the half-filled subshell notion, which atoms do not care about, and is still consistent with experimental data.