In a ground-state #"P"# atom in the gas phase, how many electrons have the quantum numbers #n = 3, l = 1, m_l = –1# ?
1 Answer
One electron.
Explanation:
The key here is the electron configuration of a neutral atom of phosphorus, which looks like this
#"P: " 1s^2 2s^2 2p^6 3s^2 3p^3#
Now, the
This means that all the three
Notice that phosphorus has
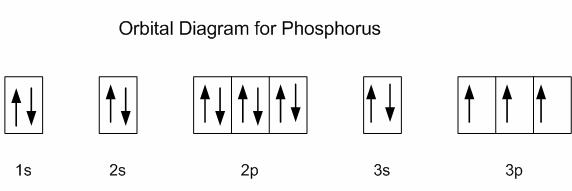
Now, you know that the principal quantum number,
In your case, you have
#n=3 -># the third energy shell
The angular momentum quantum number,
You know that you have
#l = 0 -># the#s# subshell#l = 1 -># the#p# subshell#l = 2 -># the#d# subshell
#vdots#
and so on. In your case, you're dealing with the
Finally, the magnetic quantum number,
#l = 1 implies m_l = {-1, 0 , +1}#
In your case, you have
#m_l = -1#
which refers to one of the three orbitals present in the
#n = 3, l =1, m_l = -1#
describes one electron present in the third energy shell, in the


