Question

In an isosceles triangle with legs that are 1 unit long, the angles are 45 degrees, 67.5 degrees and 67.5 degrees What is its area?

Answer 1

approximately `0.35` square units

Explanation:

To find the area, we first need to find the height of the triangle, since the formula for area of a triangle is :

`Area_"triangle"=(base*height)/2`

First, we divide the isosceles triangle into `2` right triangles.

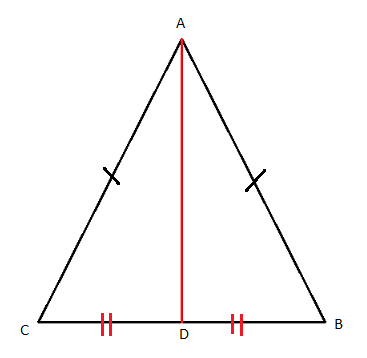
Since we know that all right triangles have one `90^@` angle and that all triangles have a `180^@` sum of interior angles, then `/_CAD` must be:

`/_CAD=180^@-90^@-67.5^@`
`/_CAD=22.5^@`

Using the Law of Sines, we can calculate the height of the right triangle:

`a/sinA=b/sinB=c/sinC`

`1/(sin90^@)=b/sin67.5^@`

`b*sin90^@=1*sin67.5`

`b*1=0.92`

`b=0.92`

Since we do not yet know the base length of the right triangle, we can also use the Law of Sines to find the base:

`a/sinA=b/sinB=c/sinC`

`1/(sin90^@)=c/sin22.5^@`

`c*sin90^@=1*sin22.5`

`c*1=0.38`

`c=0.38`

To find the base of the whole triangle, multiply the right triangle's base length by `2`:

`c=0.38*2`
`c=0.76`

Now that we have the base length and the height of the whole triangle, we can substitute these values into the formula for area of a triangle:

`Area_"triangle"=(base*height)/2`

`Area_"triangle"=((0.76)*(0.92))/2`

`Area_"triangle"=0.7/2`

`Area_"triangle"~~0.35`

`:.`, the area of the triangle is approximately `0.35` square units.