In isosceles triangle has congruent sides of 20 cm. The base is 10 cm. How do you find the height of the triangle?
3 Answers
Half the base measurement and use Pythagoras.
Let height =
Explanation:
We know that the side lengths are both 20cm (isosceles triangle).
Therefore, we can use this fact to find the midpoint of the base. This is useful as if you draw it out, you can make a right angled triangle where you can Pyhtagoras with the shorter length formula.
Now using Pythagoras short side theorem
Explanation:
You could use Heron's Formula, get the area, and then get the height, or use Pythagoras Theorem:
I'll show you both.
Pythagoras' Theorem (shorter way):
Divide the isosceles triangle into two, down the middle. Now, two right-angled triangles are formed, of sides
Heron's Formula (long route):
The area of a triangle is equal to
Here,
So now,
Obviously, the two answers do not match. This can be attributed to some rounding mistakes, but take
Height of the triangle
Explanation:
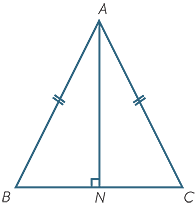
Given :
To find
Let


