Question

In Triangle MAR, how do you express `m^2` in terms of a, r, and cosM?

Answer 1

`m^2=a^2+r^2-2arcosM`

Explanation:

Let the triangle be as shown below. Here, we have drawn `RP` perpendicular to `MA`.

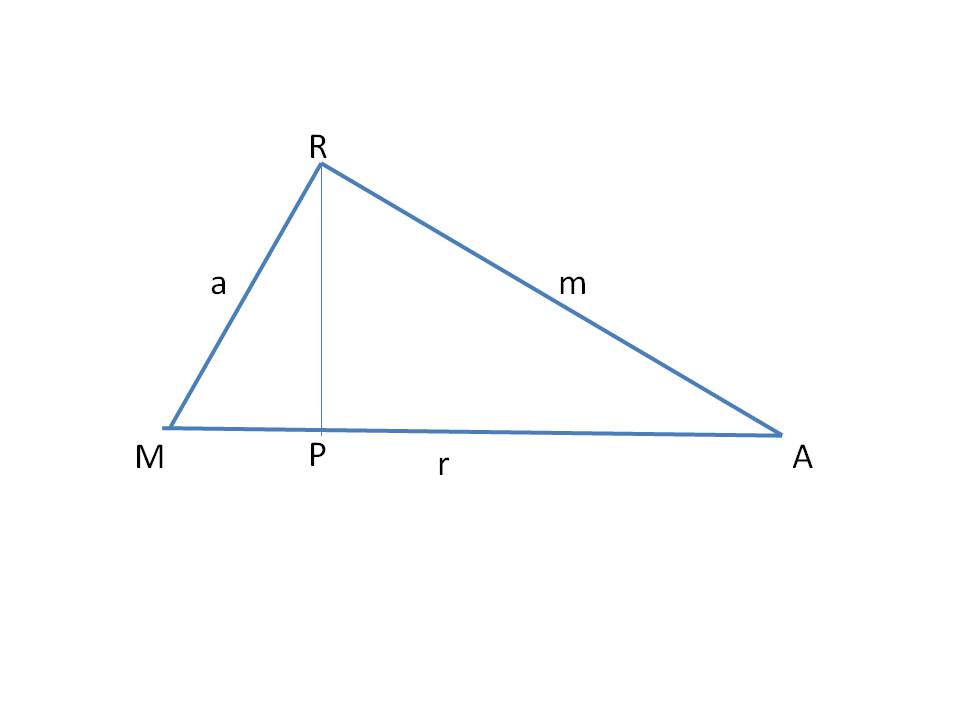
Here we have used Pythogoras theorem in initial calculations.

`m^2=RP^2+PA^2=(RM^2-MP^2)+(MA-MP)^2`

= `(RM^2-MP^2)+(MA^2-2xxMAxxMP+MP^2)`

= `a^2-MP^2+r^2-2rxxMP+MP^2`

= `a^2-cancel(MP^2)+r^2-2rxxMP+cancel(MP^2)`

= `a^2+r^2-2rxxMP`

But as `cosM=(MP)/(RM)`, hence `MP=RMxxcosM=acosM`

Therefore `m^2=a^2+r^2-2arcosM`