Is #C_2^+# paramagnetic or diamagnetic? Is #C_2# paramagnetic or diamagnetic?
1 Answer
Apr 5, 2016
From bottom to top, we have the following valence MOs:
#\mathbf(sigma_(2s))# , generated from the linear combination#2s_A + 2s_B# (head-on, in-phase)#\mathbf(sigma_(2s)^"*")# , generated from the linear combination#2s_A - 2s_B# (head-on, out-of-phase)#\mathbf(pi_(2p_x))# , generated from the linear combination#2p_(x,A) + 2p_(x,B)# (sidelong, in-phase)---degenerate with (4)#\mathbf(pi_(2p_y))# , generated from the linear combination#2p_(y,A) + 2p_(y,B)# (sidelong, in-phase)---degenerate with (3)#\mathbf(sigma_(2p_z))# , generated from the linear combination#2p_(z,A) + 2p_(z,B)# (head-on, in-phase)#\mathbf(pi_(2p_x)^"*")# , generated from the linear combination#2p_(x,A) - 2p_(x,B)# (sidelong, out-of-phase)---degenerate with (7)#\mathbf(pi_(2p_y)^"*")# , generated from the linear combination#2p_(y,A) - 2p_(y,B)# (sidelong, out-of-phase)---degenerate with (6)#\mathbf(sigma_(2p_z)^"*")# , generated from the linear combination#2p_(z,A) - 2p_(z,B)# (head-on, out-of-phase)
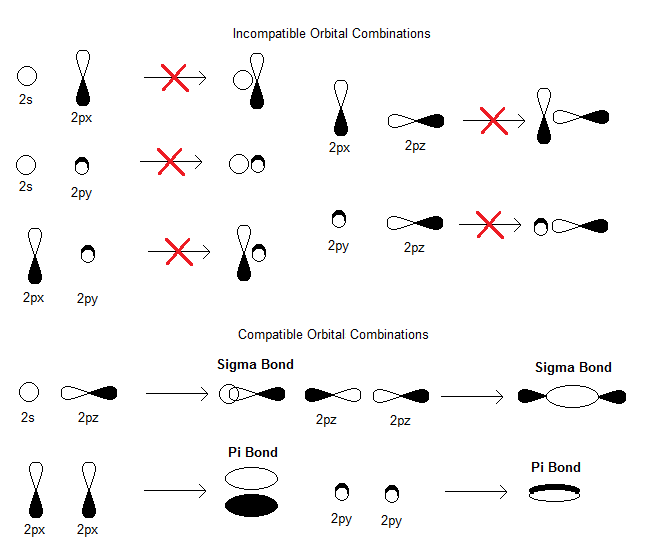
You can see the compatible bonding orbital combinations here (reverse one of the orbitals' signs to achieve the corresponding antibonding orbital combination):
As a result, we have the following MO diagram (with atomic orbital energies from Inorganic Chemistry, Miessler et al., pg. 134):
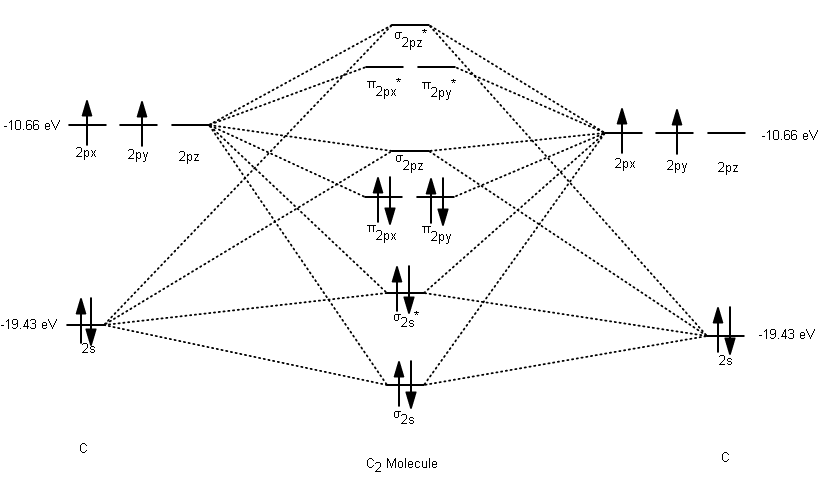
Thus, with no unpaired electrons, neutral
If

