Question

It is given that line MO = line TR and line NP = line QS, where MNOP and TQRS are parallelograms. A student has said that if those statements are true, then MNOP = TQRS. Why is this student incorrect?

Answer 1

The student is incorrect and for parallelograms to be equal, included angles between them too should be equal.

Explanation:

When two quadrilaterals `MNOP=TQRS`, then not only all corresponding sides are equal, all corresponding angles too are equal.

As `MNOP` and `TQRS` are parallelograms their diagonals bisect each other. And as `MO=TR` and `NP=QS`, it is apparent (see figure below) that `MX=XO=TY=YR` and `NX=XP=SY=YQ`.

And hence two sides of all the four triangles (in each of the parallelogram) are equal.

However, the angles included between the two diagonals can change (as is seen from the figure below),

and hence `MNOP!=TQRS`

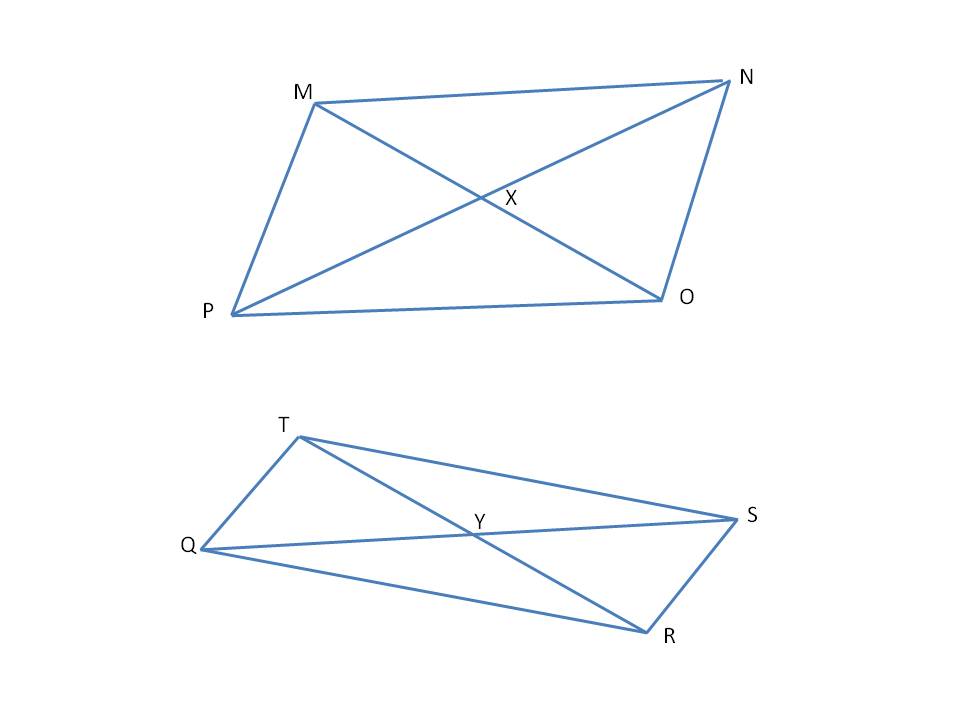
Hence, the student is incorrect and for parallelograms to be equal, included angles between them too should be equal.