Question

Kindly solve these 2 questions?

(a) If a circle is inscribed in a right angled triangle ABC with the right angle at B, show the diameter of the circle is equal to AB + BC – AC.

(b) If a triangle is inscribed in a circle, then the product of any two sides of the triangle is equal to the product of the diameter and the perpendicular distance of the third side from the opposite vertex. Prove the above statement.

Answer 1

(a)

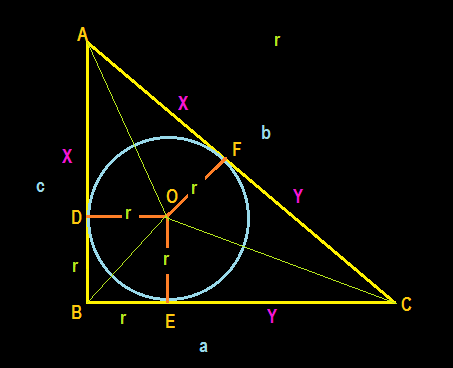
O is the center of in-circle of the right angled triangle `ABC` in which `/_ABC=90^@`

O being the in-center of the `DeltaABC`

`DeltaAODcongAOF`

So `AD=AF`

`OD=OF=r("radius of incircle")`

`DeltaCOEcongCOF`

So `CE=CF`

`OE=OF=r("radius")`

`DeltaBODcongBOE`

So `BD=BE`

`OD=OF=r("radius")`

Again `/_DBE=/_ABC=90^@`

Hence `BDOE" is a square"`

Now

`AB+BC-AC`
`=(BD+AD)+(BE+CE)-(AF+FC)`

`=(BD+BE)+AD-AF+CE-CF`

`=(r+r)+AD-AD+CE-CE`

`=2r="Diameter of the incircle"`

(b)

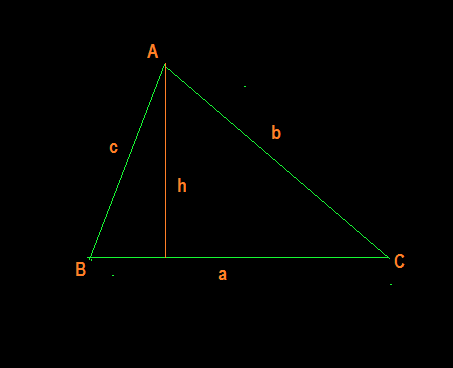
By sine law we have for `DeltaABC`

`a/sinA=b/sinB=c/sinC=2R.......[1]`,

where R is the radius of the circumcircle of `DeltaABC`

Now from relation [1] we have

`b=2RsinB`

`=>bc=2RcsinB`

`=>bc=2Rcxxh/c`,

where h is the length of the perpendicular from A to BC

So

`=>bc=2Rxxh`

`="diameter" xx" length of the perpendicular from A to BC"`

This relation can be proved similarly for any pair of sides of `DeltaABC`

So for a triangle inscribed in a circle, the product of any two sides of the triangle is equal to the product of the diameter and the perpendicular distance of the third side from the opposite vertex