Math formatting "Pro tips" edition: Long division at long last! -"?"
1 Answer
Here's my version of the long division format!
Explanation:
Ok, I've been working on this on and off for a couple of days now, ever since Ernest posted his technique here, and I think I finally came up with something very cool and very simple to write, too!
The technique is built around fractions and invisible characters. In a nutshell, you will use fractions and color(white)() to build the long division format line by line.
Before going into the fractions, it's worth noting that the color function works by breaking up the default black text color. So something like
- without the hashtags
x^2 + color(red)(3x) + 2
- with the hashtags
#x^2 + color(red)(3x) + 2#
is equivalent to
- without the hashtags
color(black)(x^2 + color(red)(3x) + 2)
- with the hashtags
#color(black)(x^2 + color(red)(3x) + 2)#
Of course, this implies that I can break up other color functions by using color(black)() to return to the default text color
- without the hashtags
color(red)(x^2 + color(black)(3x) + 2
- with the hashtags
#color(red)(x^2 + color(black)(3x) + 2#
Now, let's say that you have two fractions
#(a + b + c)/(a + b + c)" "# and#" "(d + e + f)/(d + e + f)#
If I were to write these two fractions one after the other, i.e. without any spaces between them, i would get
#(a + b + c)/(a + b + c)(d + e + f)/(d + e + f)#
Now notice what happens when I use color(white)() to make the numerators invisible
#color(white)((a + b + c))/(a + b + c) color(white)((d + e + f))/(d + e + f)#
Now look what happens when I have a fraction completely invisible and use color(black)() to make the denominator visible
- without the hashtags
color(white)( (a + b + c)/color(black)(a + b + c))color(white)((d + e + f))/(d + e + f)
- with the hashtags
#color(white)( (a + b + c)/color(black)(a + b + c))color(white)((d + e + f))/(d + e + f)#
Finally, adding a ")" to the denominator of the second fraction will get me
- without the hashtags
color(white)( (a + b + c)/color(black)(a + b + c))color(white)((d + e + f))/(")" color(white)(x)d + e + f)
- with the hashtags
#color(white)( (a + b + c)/color(black)(a + b + c))color(white)((d + e + f))/(")" color(white)(x)d + e + f)#
Now, to demonstarte this further, I'll use a solved example - I picked this one.
So, let's say that you have to write the long division format for
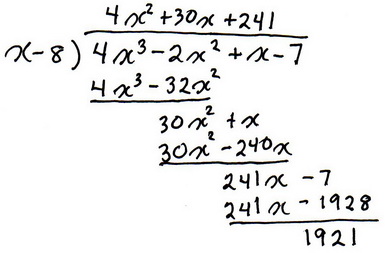
You would then pair up lines to match the fraction format. To make things clear, I'll use red text to show where the white characters would be used.
- without the hashtags
color(red)( (x-8)/color(black)(x-8)) color(red)( (4x^3 - 2x^2 + x - 7))/( ")" color(red)(")")4x^3 - 2x^2 + x - 7)
- with the hashtags - using red
- with the hashtags - using white
Now set up your fraction pairs. The second segment will start from
#(4x^3 - 32x^2)/(4x^3 + 30x^2)x/(+x)#
- without the hashtags
(4x^3 - 32x^2)/(color(red)(4x^3 +) 30x^2) color(red)(x/color(black)(+x))
- with the hashtags - using red
- with the hashtags - using white
The next two-line segment is
- with the hashtags - using red
- with the hashtags - using white
The last two-line segment is
- with the hashtags - using red
- with the hashtags - using white
Finally, put all these together to get
- with the hashtags - using red
To space these out, use color(white)() in the beginning of every code line
- with the hashtags - using red
- with the hashtags - using white
Finally, use color(black)() to add the terms you need in the numerator of the first fraction
- without the hashtags
color(red)( (x-8)/color(black)(x-8)) color(red)( (color(black)(4x^3 + 30x) x color(black)(+241)))/( ")" color(red)(")")4x^3 - 2x^2 + x - 7)
- with the hashtags - using red
- with the hashtags - using white
The final product will look like this
- with the hashtags- using red
- with the hashtags - using white
Now, as you would imagine, each long division example will have its specific spacing issues, so you're going to have to use color(white)() to create spacing as needed.
So basically, once you set up your fraction pairs, you're good to go!

