My car has an internal volume of 2600 liters. Assume the pressure was initially 760 mm Hg. If the sun heats my car from a temperature of 20° C to a temperature of 55“ C, what will the pressure inside my car be?
1 Answer
Explanation:
The idea here is that the volume of the car and the number of moles of gas you have in the car remain unchanged.
When volume and number of moles are kept constant, pressure and temperatue have a direct relationship - this is known as Gay Lussac's Law.
In simple terms, when the temperature of the gas increases, pressure increases as well. Likewise, when the temperature of the gas decreases, pressure decreases as well.
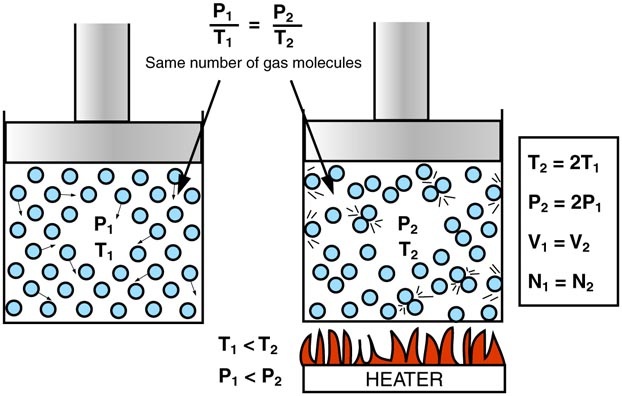
Mathematically, this is written as
#P_1/T_1 = P_2/T_2" "# , where
When plugging in your values into this equation, don't forget to convert the temperature from degrees Celsius to Kelvin.
So, rearrange and solve for
#P_2 = T_2/T_1 * P_1#
#P_2 = ((273.15 + 55)color(red)(cancel(color(black)("K"))))/((273.15 + 20)color(red)(cancel(color(black)("K")))) * "760 mmHg" = "850.74 mmHg"#
I'll leave the answer rounded to one sig fig, despite the fact that you only gave one sig fig for the initial temperature of the gas
#P_2 = color(green)("850 mmHg")#

