On earth a tank is 10.0L in size, has a pressure of 50ATM and a temperature of 23 degrees celsius. When the rocket gets near the sun, the temperature increases to 225 degrees celsius. If the tank bursts at 100ATM, will it burst?
1 Answer
No, it will not burst.
Explanation:
The trick here is to recognize the fact that the amount of gas in the tank remains constant.
Moreover, the volume of the gas tank remains constant as well, which is why you're trying to determine whether or not it will burst at the new temperature.
So, when the amount of gas and the volume it occupies remain constant, pressure and temperature have a direct relationship - this is known as Gay Lussac's Law.
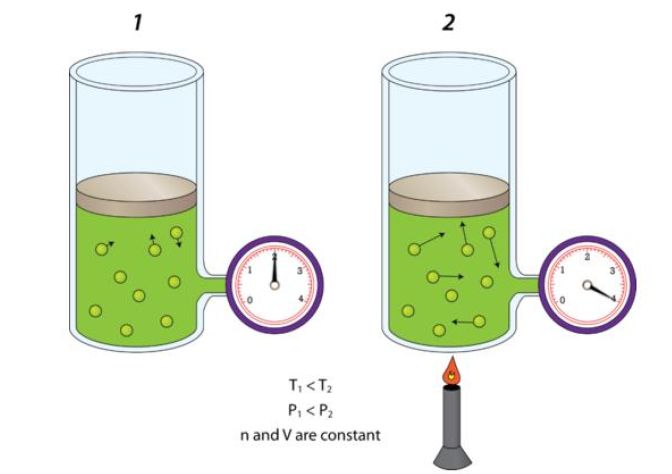
In other words, if temperature increases, then you can expect pressure to increase as well. Likewise, if temperature decreases, pressure will decrease as well.
This happens because as the temperature increases, the average kinetic energy of the gas molecules increases as well. As a result, the gas molecules will hit the walls of the container more frequently and with more force
Mathematically, this is written as
#P_1/T_1 = P_2/T_2" "# , where
So, plug in your values and solve for
#P_1/T_1 = P_2/T_2 implies P_2 = T_2/T_1 * P_1#
#P_2 = ((273.15 + 225)color(red)(cancel(color(black)("K"))))/((273.15 + 23)color(red)(cancel(color(black)("K")))) * "50 atm" ~~ "84 atm"#
Since this pressure is smaller than the limit pressure of

