Suppose a parabola has vertex (4,7) and also passes through the point (-3,8). What is the equation of the parabola in vertex form?
1 Answer
Actually, there are two parabolas (of vertex form) that meet your specifications:
Explanation:
There are two vertex forms:
where
We are given no reason to exclude one of the forms, therefore we substitute the given vertex into both:
Solve for both values of a using the point
Here are the two equations:
Here is an image containing both parabolas and the two points:
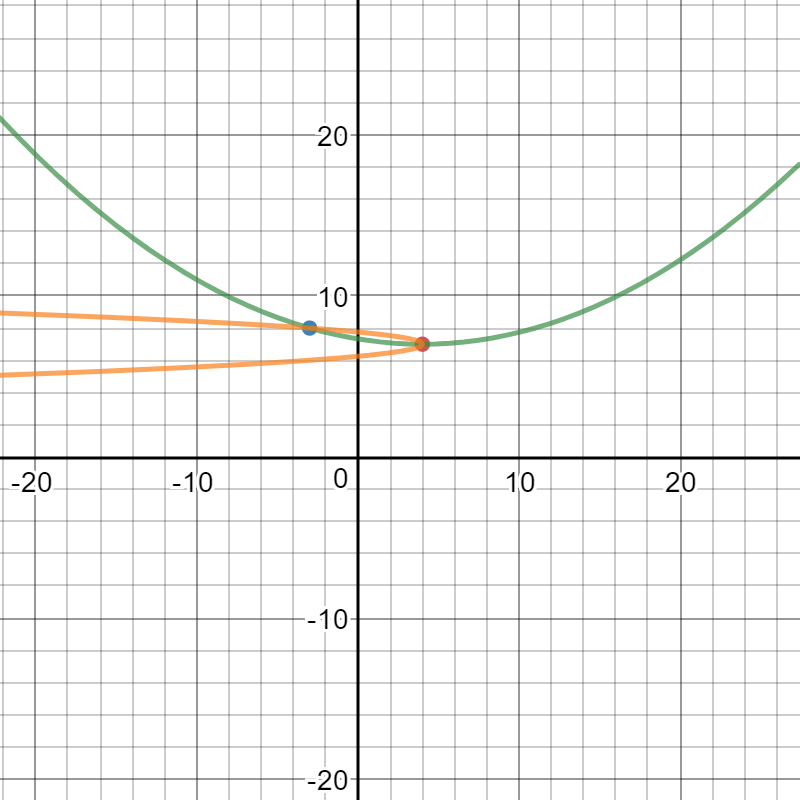
Please observe that both have the vertex
