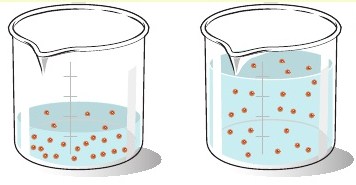
Suppose you have 125.0 mL of 0.400 M #NaCl# solution. This is too salty, so you dilute it by adding another 50.0 mL of water. What is the new concentration of #NaCl# in units of molarity?
1 Answer
Explanation:
This is a great example of a practice problem that requires you to use the formula for dilution calculations.
To make it more interesting, let's assume that you're not familiar with that problem.
The most important thing to remember about a dilution is the the number of moles of solute must remain constant.
That is, the number of moles of solute present in the initial solution must be equal to the number of moles of solute present in the diluted solution.
Since molarity is defined as moles of solute per liter of solution, keeping the number of moles of solute constant allows you to decrease concentration by increasing the total volume of the solution.
So, use the molarity and volume of the initial solution to determine how many moles of sodium chloride it contains
#color(blue)(| bar(ul(c = n/V))| implies n = c * V#
#n_(NaCl) = "0.400 M" * 125.0 * 10^(-3)"L" = "0.0500 moles NaCl"#
This is exactly how many moles of solute you must have in the diluted solution.
The new volume of the solution will be
#V_"new" = "125.0 mL" + "50.0 mL" = "175.0 mL"#
This means that the molarity of the diluted solution will be
#c = "0.0500 moles"/(175.0 * 10^(-3)"L") = color(green)(|bar(ul("0.286 M")|)#
Now, this is exactly what the formula for dilutions calculations allows you to do
#color(blue)(overbrace(c_1 xx V_1)^(color(purple)("moles of solute in initial solution")) = overbrace(c_2 xx V_2)^(color(purple)("moles of solute in diluted solution")))#
Here
Rearrange to solve for
#c_2 = V_1/V_2 xx c_1#
#c_2 = (125.0 color(red)(cancel(color(black)("mL"))))/(175.0color(red)(cancel(color(black)("mL")))) * "0.400 M" = color(green)(|bar(ul("0.286 M")|)#
The answer is rounded to three sig figs.