Question

The activation energy of a certain reaction is 46.6 kj/mol. At 20 degrees Celsius the rate constant is `0.0130s^-1`. At what temperature would this reaction go twice as fast (T2)?

Answer 1

At `31^@"C"`

Explanation:

We can use The Arrhenius Equation:

`k=Ae^(-E_a/(RT))`

`k` is the rate constant

`A` is the frequency factor and is constant

`R` is the gas constant and `= 8.31"J""/""K""/""mol"`

`E_a` is the activation energy

`T` is the absolute temperature.

A more usable form of the equation is obtained by taking natural logs of both sides `rArr`

`lnk=lnA-E_a/(RT)`

If the reaction occurs at two temperatures `T_1` and `T_2` then we can write:

`lnk_1=lnA-E_a/(RT_1)" "color(red)((1))`

`lnk_2=lnA-E_a/(RT_2)" "color(red)((2))`

Now we can subtract both sides of `color(red)((1))` and `color(red)((2))rArr`

`ln(k_1/k_2)=-E_a/(RT_1)+E_a/(RT_2)`

Since we know that `k_2=2k_1` this becomes:

`ln(1/2)=E_a/R[1/T_2-1/T_1]`

#:.-0.693=(46.6xx10^3)/ 8.31[1/T_2-1/293]#

`:.1/T_2-1/293=-1.235xx10^-4`

`:.1/T_2=-1.245xx10^-4+34.13xx10^-4=34.13xx10^-4`

`:.T_2=304color(white)x"K"`

`:.T_2=304-273=34^@"C"`

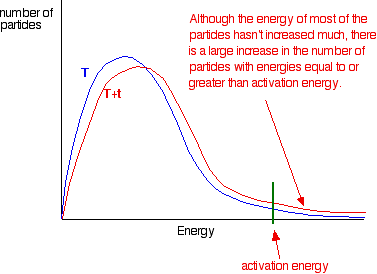
This shows how a rise of just 14 degrees can double the rate of reaction.

The graphic below shows how a small increase in temperature results in a large increase in the number of particles which have the minimum energy for a reaction to happen: