The area of a circle inscribed in an equilateral triangle is 154 square centimeters. What is the perimeter of the triangle? Use pi=22/7 and square root of 3= 1.73.
1 Answer
Jan 6, 2016
Perimeter
Explanation:
This is Geometry, so lets look at at a picture of what we are dealing with:
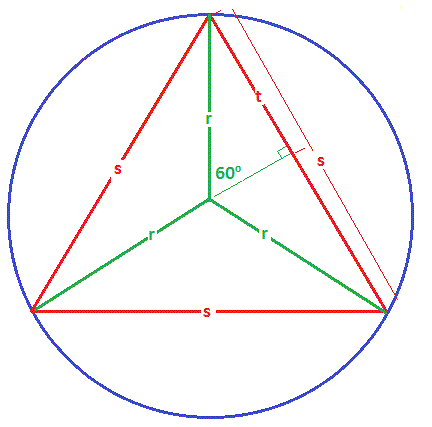
We are told
and to use
If
and
Perimeter
