Question

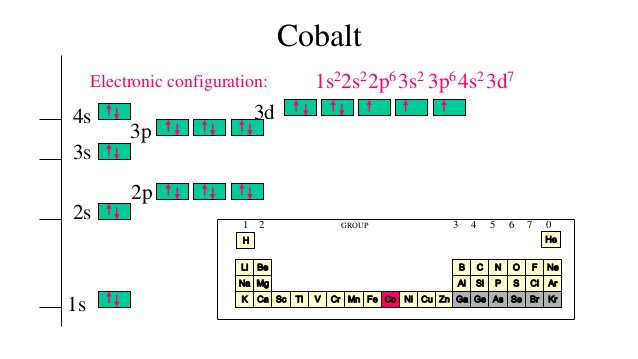
The atom cobalt has 27 electrons. How many energy levels will its electrons use?

Answer 1

Four energy levels.

Explanation:

The number of electrons each energy level can hold increases as you add more and more energy levels to an atom.

The relationship that exists between the energy level, `n`, and the number of electrons it can hold can be written like this

`color(blue)(|bar(ul(color(white)(a/a)"no. of e"^(-) = 2n^2color(white)(a/a)|)))`

You can use this equation to find the maximum number of electrons that can be added to each energy level. You will have

• the first energy level, `n=1`

`"no. of e"^(-) = 2 * 1^2 = "2 e"^(-)`

• the second energy level `n=2`

`"no. of e"^(-) = 2 * 2^2 = "8 e"^(-)`

• the third energy level, `n=3`

`"no. of e"^(-) = 2 * 3^2 = "18 e"^(-)`

• the fourth energy level, `n=4`

`"no. of e"^(-1) = 2 * 4^2 = "32 e"^(-)`

and so on.

In your case, cobalt, `"Co"`, is said to have a total of `27` electrons surrounding its nucleus. These electrons will be placed in orbitals in order of increasing energy in accordance to the Aufbau Principle.

Now, it's very important to remember that when you're adding electrons to an atom, the 3d-orbitals, which are located on the third energy level, are higher in energy than the 4s-orbital.

This means that you must fill the 4s-orbital first, then distribute the rest of the electrons to the 3d-orbitals.

So, a neutral cobalt atom will have

`n=1 -> "2 e"^(-)` in the `1s` subshell

`n=2 -> "8 e"^(-)` in the `2s` and `2p` subshells

Now, these two energy levels will hold

`"2 e"^(-) + "8 e"^(-) = "10 e"^(-)`

Now comes the tricky part. The third energy level can hold `"18 e"^(-)`, so in theory it can hold the remaining

`"27 e"^(-) - "10 e"^(-) = "17 e"^(-)`

that the neutral cobalt atom has. You could thus say that

`color(red)(cancel(color(black)(n=3 -> "17 e"^(-))))` in the `3s`, `3p`, and `3d` subshells

and conclude that the electrons that surround the nucleus of a cobalt atom are spread out on `3` energy levels. You would be wrong.

Taking it one subshell at a time, you will have

`"2 e"^(-) ->` in the `3s` subshell

`"6 e"^(-) ->` in the `3p` subshell

You now have

`"17 e"^(-) - ("2 e"^(-) + "6 e"^(-)) = "9 e"^(-)`

to distribute. Because the 4s orbital is filled before the 3d-orbitals, the next two electrons are going to be distributed on the fourth energy level

`n=4 -> "2 e"^(-)` in the `4s` subshell

The remaining `"7 e"^(-)` will now be distributed in the 3d-subshell.

Therefore, a neutral cobalt atom will have

`n=1 -> "2 e"^(-)` in the `1s` subshell

`n=2 -> "8 e"^(-)` in the `2s` and `2p` subshells

`n= 3 -> "15 e"^(-)` in the `3s`, `3p`, and `3d` subshells

`n=4 -> "2 e"^(-)` in the `4s` subshell