Question

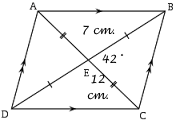
The diagonals of a parallelogram intersect at 42 degree angle and have lengths 12 and 7cm. How do you find the lengths of the sides of the parallelogram? See diagram.

Answer 1

The sides measure `4.13" cm."` and `15.35" cm."`.

Explanation:

We know the length of BD and of AC. However, we don't have an angle that is on the exterior (ex BDC, BCD or DBC), so we don't have enough information to use Cosine's Law. We will approach this problem by a different approach.

We know, by the properties of the parallelogram, that diagonals are cut into two equal parts at the point of intersection. Hence, if `AC = 12" cm"`, then `EC = 6" cm"`. Similarly, if `BD = 7" cm"`, then `BE = 3.5" cm"`.

We can now use the Law of Cosines to solve for side `BC`.

`BC^2 = EC^2 + BE^2 - 2(EC)(BE)cos/_BEC`

`BC^2 = 6^2 + 3.5^2 - (2 xx 6 xx 3.5 xx cos(42˚))`

`BC ~= 4.13" cm."`

To find the length of `DC`, we can use the property that `/_BEC` and `/_DEC` are supplementary, or their sum is `180˚`.

`/_BEC + /_DEC = 180˚`

`42˚ + /_DEC = 180˚`

`/_DEC = 138˚`

Since `BE = ED`, we can use the Law of Cosine's once more.

`DC^2 = DE^2 + EC^2 - (2 xx DE xx EC xx cos(/_DEC))`

`DC^2 = 3.5^2 + 6^2 - (2 xx 3.5 xx 6 xx cos(138˚))`

`DC ~= 15.35" cm."`

Hence, the two sides of the parallelogram measure `4.13" cm."` and `15.35" cm."`.

Hopefully this helps!