The total profit function P(x) for a company producing x thousand units is given by P(x) = -3x^2 + 36x - 81. How do you find the values of x for which the company makes a profit?
1 Answer
Jul 24, 2015
I found:
Explanation:
You can try plotting your function considering that it represents a parabola:
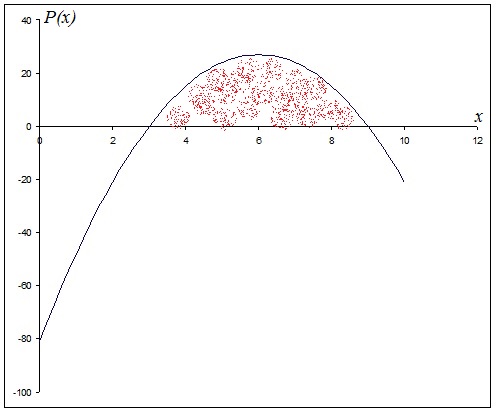
You can see that producing zero units (
There is a region where

