Question

Three circles with radii 4, 5, 6cm respectively are tangent to each other externally. How do you find the angles of the triangle whose vertexes are the centers of the circles?

Answer 1

Three angles are `50.48^o,58.99^o` and `70.53^o`.

Explanation:

Three circles with radii `4`, `5` and `6` form a triangle, whose sides are sum of their radii in pairs.

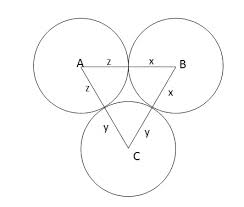
Hence sides of triangle are `4+5`, `4+6` and `5+6`, i.e. `9`, `10` and `11`.

To find interior angles, we should solve this triangle.using cosine formula `cosC=(a^2+b^2-c^2)/(2ab)`

Hence `cosC=(9^2+10^2-11^2)/(2xx9xx10)=(81+100-121)/180=60/180=1/3`
and `C=70.53^o`

Similarly `cosA=(10^2+11^2-9^2)/(2xx10xx11)=(100+121-81)/220=140/220=7/11`
and `A=50.48^o`

and `cosB=(9^2+11^2-10^2)/(2xx9xx11)=(81+121-100)/198=102/198`
and `B=58.99^o`

Hence, three angles are `50.48^o,58.99^o` and `70.53^o`.