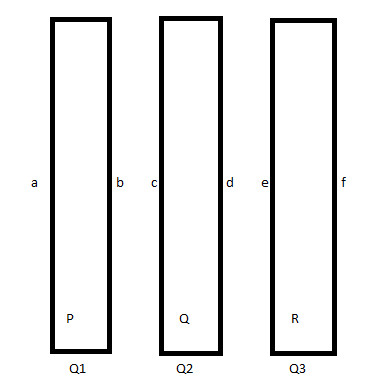
Three metallic plates each of area A are kept as shown in figure and charges #q_1,q_2,q_3# are given to them find the resulting charge distribution on the six surfaces , neglecting edge effect ?
1 Answer
The charges on the faces a, b, c ,d, e and f are
Explanation:
The electric field in each region can be found using Gauss law and superposition. Assuming the area of each plate to be
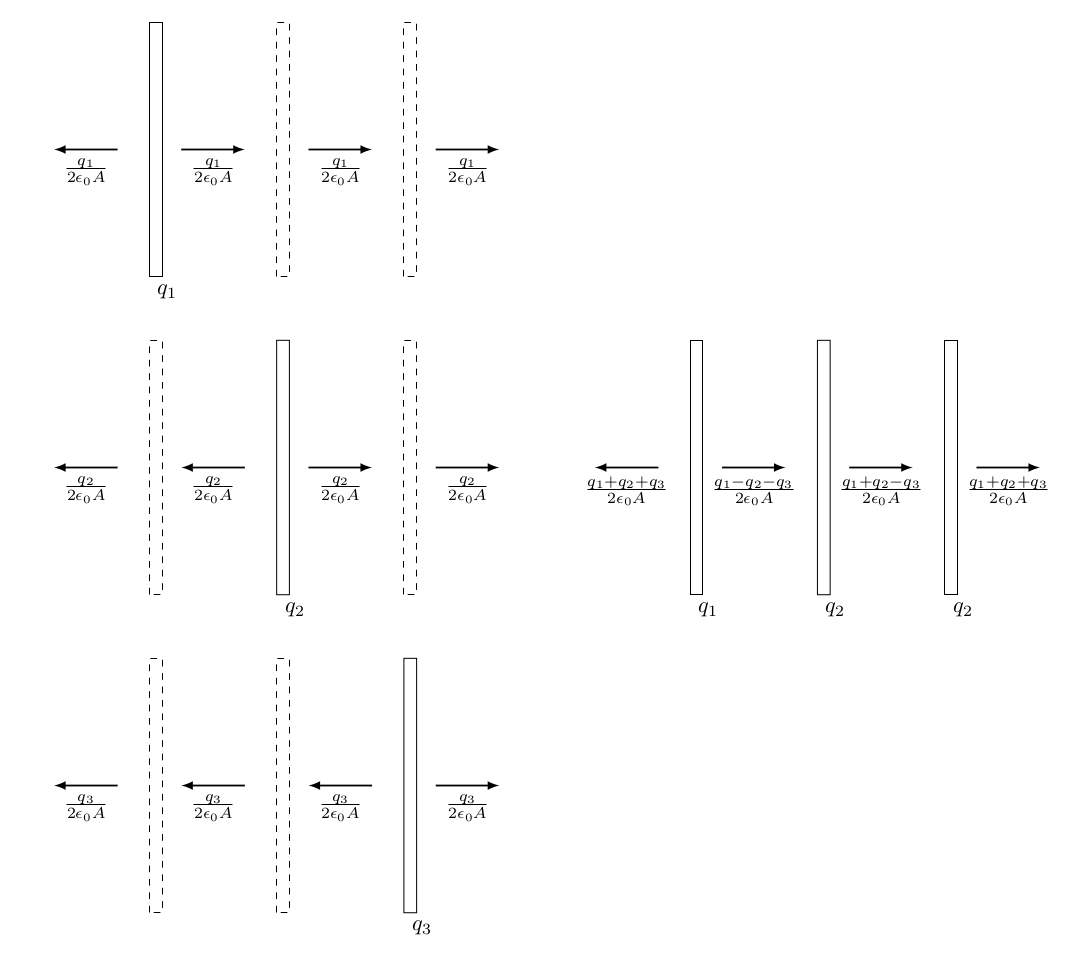
The figure above shows the the fields when only one of the three plates are charged, in succession, on the left and : the total fields, derived using superposition, on the right.
Once we have the fields, the charges on each faces can be easily found from Gauss law. For example, taking a Gaussian surface in the form of a right cylinder that has one of its circular faces inside the leftmost conducting plate, and the other one sticking out in the region to the left of it, will give you the surface charge density on the face

