Two circles have the following equations #(x -1 )^2+(y -7 )^2= 25 # and #(x +3 )^2+(y +3 )^2= 49 #. Does one circle contain the other? If not, what is the greatest possible distance between a point on one circle and another point on the other?

1 Answer
Douglas K.
Dec 1, 2016

The farthest possible distance between two points, one on each circle, is the sum of the two radii and the distance between the centers: #12 + sqrt(116) ~~ 22.77#

Explanation:

The first circle has a center at #(1,7)# the radius is 5
The second circle has a center at #(-3,-3)# the radius is 7

The distance, d, between their centers is:

#d = sqrt((1 - -3)^2 + (7 - -3)^2)#

#d = sqrt(4^2 + 10^2)#

#d = sqrt(116)#

The circle partially overlap but the larger does not contain the smaller. Please see the drawing:

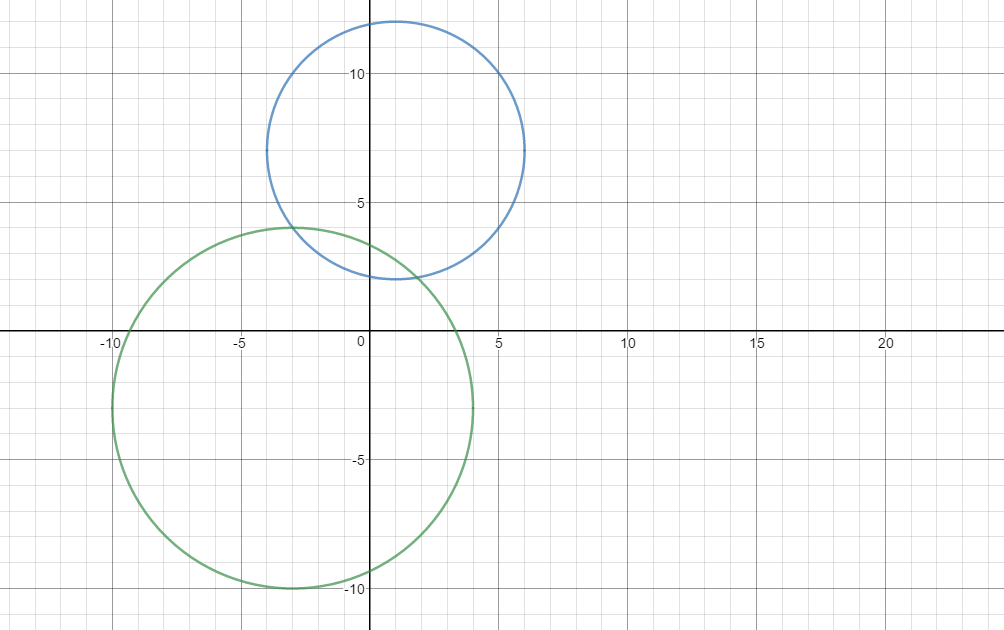
Desmos.com

The farthest possible distance between two points, one on each circle, is the sum of the two radii and the distance between the centers: #12 + sqrt(116) ~~ 22.77#

Related questions
See all questions in Equation of a Circle
Impact of this question
1311 views around the world
You can reuse this answer
Creative Commons License