Question

Two circles have the following equations: `(x +3 )^2+(y -5 )^2= 64` and `(x -7 )^2+(y +2 )^2= 25`. Does one circle contain the other? If not, what is the greatest possible distance between a point on one circle and another point on the other?

Answer 1

`color(blue)(sqrt(149)+13 " units"`

Explanation:

We know the following about two circles:

Let `d` be the distance between the circles centres.

Let `R` be the sum of the radii of the circles.

If:

`d > Rcolor(white)(888)` then the circles do not touch.

`d < Rcolor(white)(888)` Then the circles intersect at two points, or one circle is contained in the other.

`d = Rcolor(white)(888)` Then the circles touch at one point.

We have centres `(-3,5) and (7,-2)`

Using the distance formula to find distance between these centres:

`|d|=sqrt((7-(-3))^2+(-2-5)^2)=sqrt(149)`

The radii are `r_1=sqrt(64)=8 and r_2=sqrt(25)=5`

Therefore:

`sqrt(149)<13`

So the circles intersect at two points, or one is contained in the other. We can test if one is contained in the other by observing that, if this is the case then, the sum of the distance between centres and the smaller radius will be less than the larger radius.

`:.`

`d+r_2 < r_1`

`sqrt(149)+5 > 8`

The answer is therefore NO.

The greatest distance between a point on one circle and a point on the other can be found as follows.

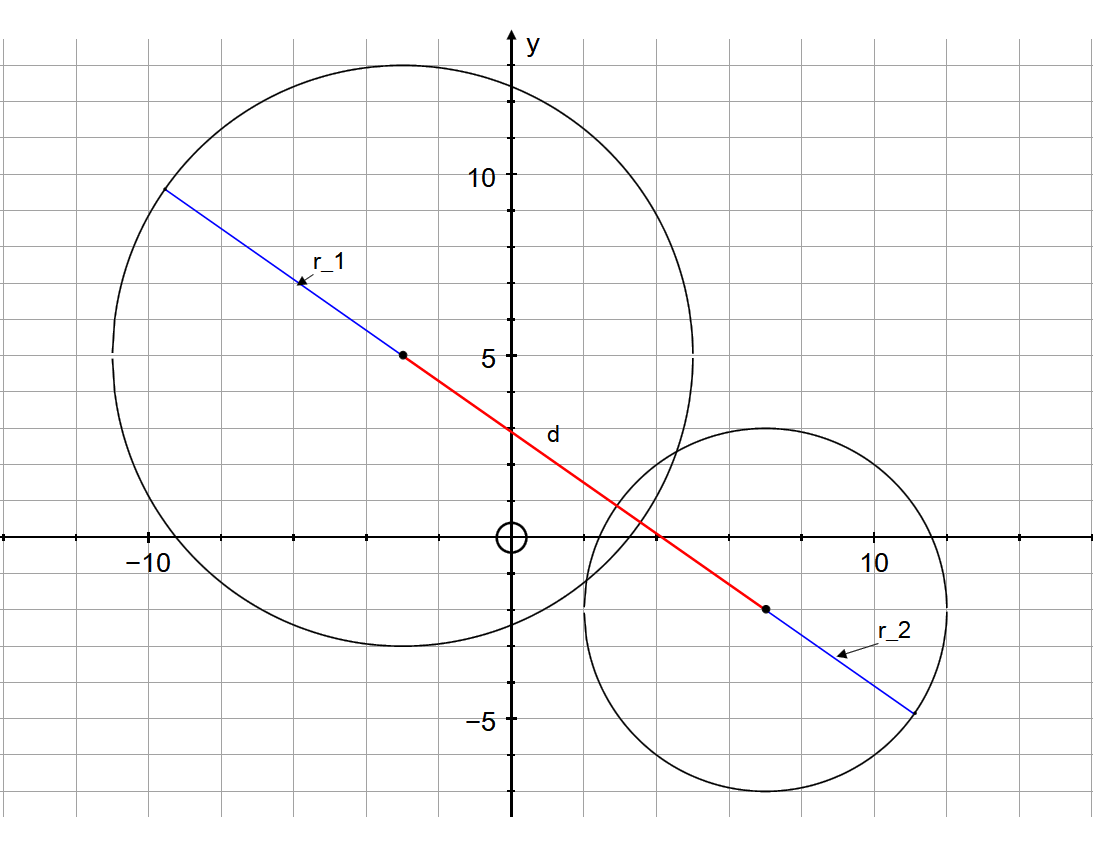
Notice from the plot that the greatest distance is when the radii of the circles are lying on the same straight line through the centres of the circles. We can see from this that the furthest distance is given by:

`d+r_1+r_2`

`sqrt(149)+8+5=sqrt(149)+13 " units"`

PLOT: