Question

Two circles have the following equations `(x +8 )^2+(y -5 )^2= 16` and `(x +4 )^2+(y +1 )^2= 49`. Does one circle contain the other? If not, what is the greatest possible distance between a point on one circle and another point on the other?

Answer 1

The largest circle doesn't contain the other.

Maximum distance:

`sqrt(113 + 40 sqrt(2) + 8 sqrt(47) + 10 sqrt(94))≈17.9267`

Explanation:

Both circles have their equation written in the form

`(x-x_0)^2+(y-y_0)^2=r^2`

which simplify our calculation, since we already know that `(x_0,y_0)` is the center and `r` is the radius. So, we already know:

First circle:
- Center: `(-8,5)`
- Radius: `sqrt(16) = 4`

Second circle:
- Center: `(-4,1)`
- Radius: `sqrt(49) = 7`

Now, if one circle includes the other, the one with the largest radius must include the one with the smaller radius, and the distance between the two centers must be less than the smaller radius. This distance is given by

`d = sqrt((-8+4)^2+(541)^2) = 4sqrt(2) > 4`

So the smallest circle is not included in the largest one.

To find the maximum distance between two of their points, consider the line passing through the two centers. It intersects the circles in four points: two couples realizing the minimum distance (the two between the centers) and the maximum distance (the two opposite to the centers).

The line passing through the centers is given by

`\frac{y-5}{1-5}=\frac{x+8}{-4+8} \to y = -x-3`

Find the intersection with circles via system:

First circle:
`y = -x-3`
`(x+8)^2+(y−5)^2=16`

Solutions:
- `P_1 = (2sqrt(2) - 8,5 - 2 sqrt(2))`
- `P_2 = (-8-2sqrt(2),5 + 2 sqrt(2))`

Second circle:
`y = -x-3`
`(x+4)^2+(y+1)^2=49`

Solutions:
- `P_3 = (-3 - sqrt(94)/2,sqrt(47/2))`
- `P_4 = (1/2 sqrt(94) - 3,-sqrt(47/2))`

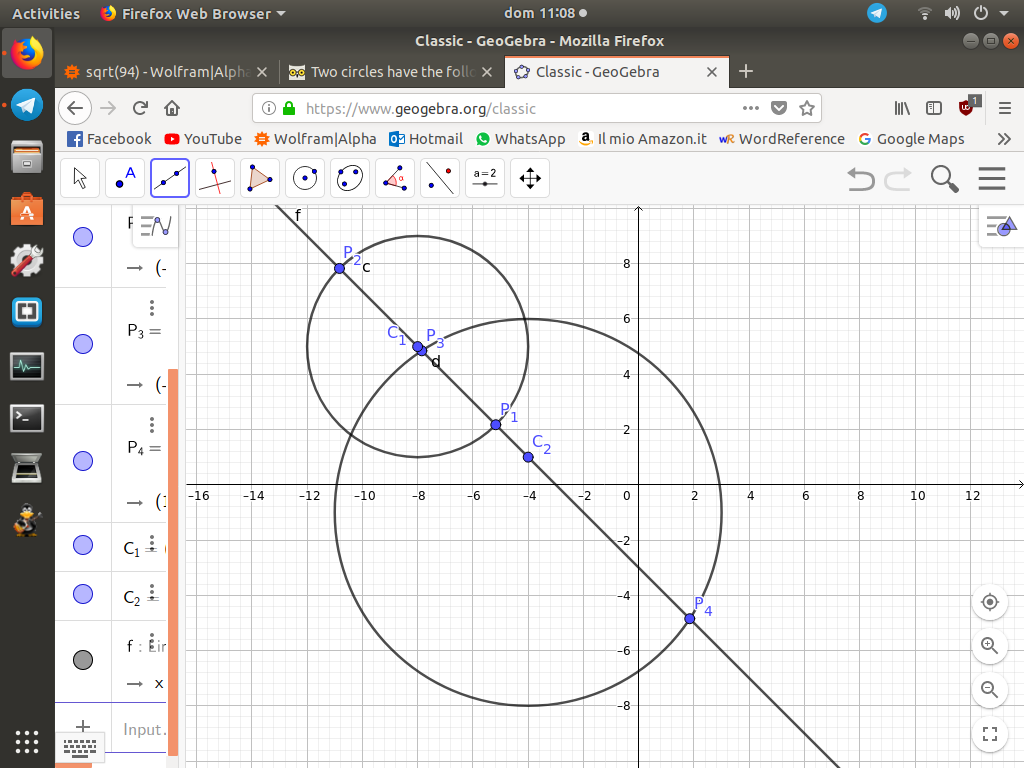
You can see from the picture that `P_2` and `P_4` are the points we're interested in. Compute their distance with the usual formula

`d = sqrt((x_1-x_2)^2+(y_1-y_2)^2)`

to get this awkward result:

`sqrt(113 + 40 sqrt(2) + 8 sqrt(47) + 10 sqrt(94))≈17.9267`