Two corners of a triangle have angles of # (2 pi )/ 3 # and # ( pi ) / 4 #. If one side of the triangle has a length of # 4 #, what is the longest possible perimeter of the triangle?
1 Answer
Explanation:
The problem gives you two out of the three angles in an arbitrary triangle. Since the sum of the angles in a triangle must add up to 180 degrees, or
Let's draw the triangle:
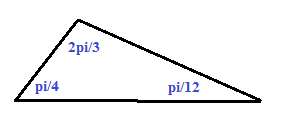
The problem states that one of the sides of the triangle has a length of 4, but it does not specify which side. However, in any given triangle, it is true that the smallest side will be opposite from the smallest angle.
If we want to maximize the perimeter, we should make the side with length 4 the side opposite from the smallest angle. Since the other two sides will be larger than 4, it guarantees that we will maximize the perimeter. Therefore, out triangle becomes:
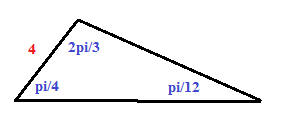
Finally, we can use the law of sines to find the lengths of the other two sides:
Plugging in, we get:
Solving for x and y we get:
Therefore, the maximum perimeter is:
Note: Since the problem does not specify the units of length on the triangle, just use "units".

