Two corners of a triangle have angles of # (2 pi )/ 3 # and # ( pi ) / 6 #. If one side of the triangle has a length of # 1 #, what is the longest possible perimeter of the triangle?

Question

2142 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-02-19T05:58:10

Perimeter of isosceles triangle #color(green)(P = a + 2b = 4.464#

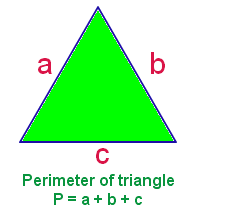
enter image source here

#hatA = (2pi)/3, hatB = pi/6, side = 1#

To find the longest possible perimeter of the triangle.

Third angle #hatC = pi - (2pi)/3 - pi/6 = pi/6#

It’s an isosceles triangle with
#hat B = hat C = pi/6#

Least angle #pi/6# should correspond to the side 1 to get the longest perimeter.

Applying sine law, #a / sin A = c / sin C#

#a = (1 * sin ((2pi)/3)) / sin (pi/6) = sqrt3 = 1.732#

Perimeter of isosceles triangle #color(green)(P = a + 2b = 1 + (2 * 1.732) = 4.464#