Two corners of an isosceles triangle are at #(1 ,6 )# and #(2 ,9 )#. If the triangle's area is #36 #, what are the lengths of the triangle's sides?
1 Answer
Explanation:
The length of the given side is
From the formula of the triangle's area:
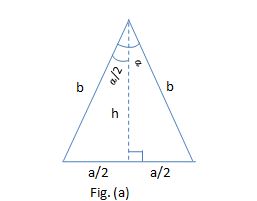
Since the figure is an isosceles triangle we could have Case 1 , where the base is the singular side, ilustrated by Fig. (a) below
Or we could have Case 2 , where the base is one of the equal sides, ilustrated by Figs. (b) and (c) below
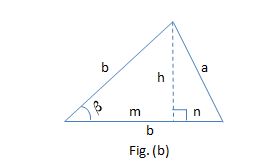
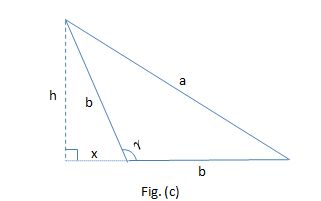
For this problem Case 1 always applies, because:
#tan(alpha/2)=(a/2)/h# =>#h=(1/2)a/tan(alpha/2)#
But there's a condition so that Case 2 apllies:
#sin(beta)=h/b# =>#h=bsin beta#
Or#h=bsin gamma#
Since the highest value of#sin beta# or#sin gamma# is#1# , the highest value of#h# , in Case 2, must be#b# .
In the present problem h is longer than the side to which it is perpendicular, so for this problem only the Case 1 applies.
Solution considering Case 1 (Fig. (a))
#b^2=h^2+(a/2)^2#
#b^2=(72/sqrt(10))^2+(sqrt(10)/2)^2#
#b^2=5184/10+10/4=(5184+25)/10=5209/10# =>#b=sqrt(520.9)~=22.823#

