Question

Two corners of an isosceles triangle are at `(3 ,9 )` and `(6 ,7 )`. If the triangle's area is `4`, what are the lengths of the triangle's sides?

Answer 1

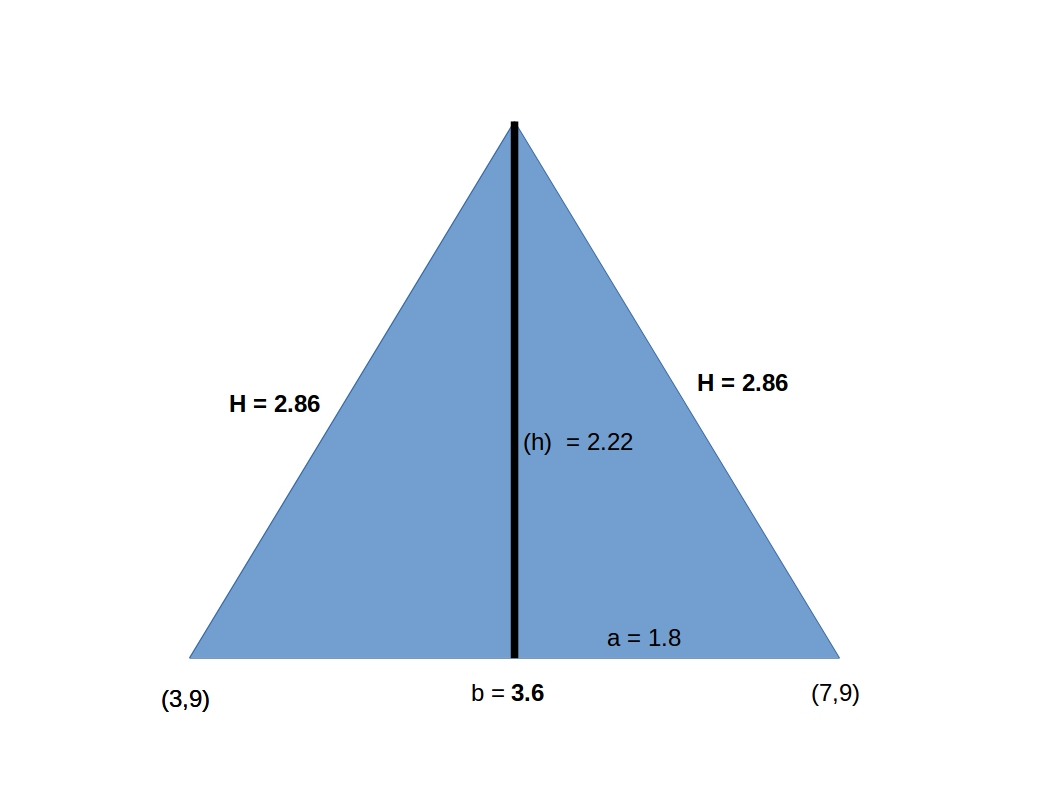
2.86, 2.86 and 3.6

Explanation:

Using the equation for a line to find the length of the known side, we then use it as the arbitrary base of the triangle with the area to find the other point.

The distance between the final point locations can be calculated from the “distance formula” for Cartesian Coordinate systems:
d= `sqrt ((x_2-x_1)^2 +(y_2-y_1)^2)`
d= `sqrt ((6 - 3)^2+(7 - 9)^2)` ; d= `sqrt ((3)^2+(-2)^2)` ; d= `sqrt ((9+4)`
d= `sqrt ((13)` = 3.6
Triangle area = ½ b * h 4 = ½ * 3.6 * h ; h = 2.22

This is the distance to the third point from the midpoint of the other points, perpendicular to the line between the given points.
For an isosceles triangle two sides must be the same length, so the one given is the third side. Each half of the isosceles triangle has two known lengths of 1.8 and 2.22 with the hypotenuse being the final length desired.

`(1.8)^2 + (2.22)^2 = H^2`
3.24 + 4.93 = `H^2`
8.17 = `H^2`
2.86 = H

The three sides are thus 2.86,2.86 and 3.6 in length.