Question

Two corners of an isosceles triangle are at `(4 ,2 )` and `(1 ,3 )`. If the triangle's area is `2`, what are the lengths of the triangle's sides?

Answer 1

Sides:
`color(white)("XXX"){3.162, 2.025, 2.025}`
or
`color(white)("XXX"){3.162,3.162,1.292}`

Explanation:

There are two cases that need to be considered (see below).

For both cases I will refer to the line segment between the given point coordinates as `b`.
The length of `b` is
`color(white)("XXX")abs(b)=sqrt((4-1)^2+(2-3)^2)=sqrt(10)~~3.162`

If `h` is the altitude of the triangle relative to base `b`
and given that the area is 2 (sq.units)
`color(white)("XXX")abs(h)=(2xx"Area")/abs(b)=4/sqrt(10)~~1.265`

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Case A: `b` is not one of the equal sides of the isosceles triangle.

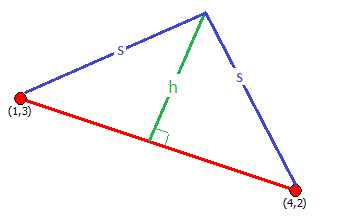
Notice that the altitude `h` divides the triangle into two right triangles.
If the equal sides of the triangle are denoted as `s`
then
`color(white)("XXX")abs(s)=sqrt(abs(h)^2+(abs(b)/2)^2~~2.025`
(using the previously determined values for `abs(h)` and `abs(b)`)

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

Case B: `b` is one of the equal sides of the isosceles triangle.

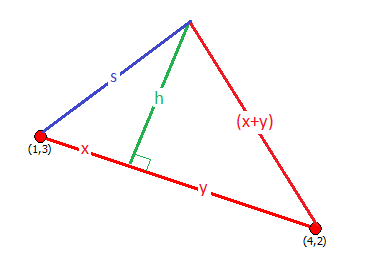
Note that the altitude, `h`, divides `b` into two sub-line segments which I have labelled `x` and `y` (see diagram above).

Since `abs(x+y)=abs(b)~~3.162`
and `abs(h)~~1.265`
(see prologue)

`color(white)("XXX")abs(y)~~sqrt(3.162^2-1.265^2)~~2.898`

`color(white)("XXX")abs(x)=abs(x+y)-abs(y)`
`color(white)("XXXX")=abs(b)-abs(y)`
`color(white)("XXXX") ~~3.162-2.898~~0.264`

and
`color(white)("XXX")abs(s)=sqrt(abs(h)^2+abs(x)^2)=sqrt(1.265^2+0.264^2)~~1.292`