They're called vertices.
I like this one because we're not told if we're given the common side or the base. Let's find the triangles that make the area 36 and figure out which are isosceles later.
Call the vertices #A(5,8), B(4,6), C(x,y).#
We can immediately say
#AB = \sqrt{ (5-4)^2 + (8-6)^2 }= sqrt{5} #
The shoelace formula gives the area
#36 = 1 / 2 | 5(6) - 8(4) + 4y - 6x + 8x - 5y | #
# 72 = | -2 + 2x - y \ | #
# y = 2x - 2 \pm 72 #
#y = 2x + 70 quad # and # quad y=2x - 74 #
That's two parallel lines, and any point #C(x,y)# on either one of them makes #text{area}(ABC)=36.#
Which are isosceles? There are three possibilities: AB is the base, BC is the base, or AC is the base. Two will have the same congruent triangles, but lets work them out:
Case AC=BC:
# (x-5)^2 + (y-8)^2 =(x-4)^2+(y-6)^2 #
# -10 x + 25 -16 y + 64 = -8x + 16 -12 y + 36#
# -2x -4 y = -37 #
That meets #y=2x + k quad quad (k=70,-74)# when
#-2x -4 (2x + k)= -37 #
# -10 x = 4k - 37 #
# x= 1/10 (37 - 4k) quad quad quad k=70,-74#
# x = 1/10(37 - 4(70)) = -24.3 #
# y = 2(-24.3) + 70 = 21.4 #
# x = 1/10 ( 37 - 4(-74)) = 33.3 #
#y = 2(33.3) - 74 = -7.4 #
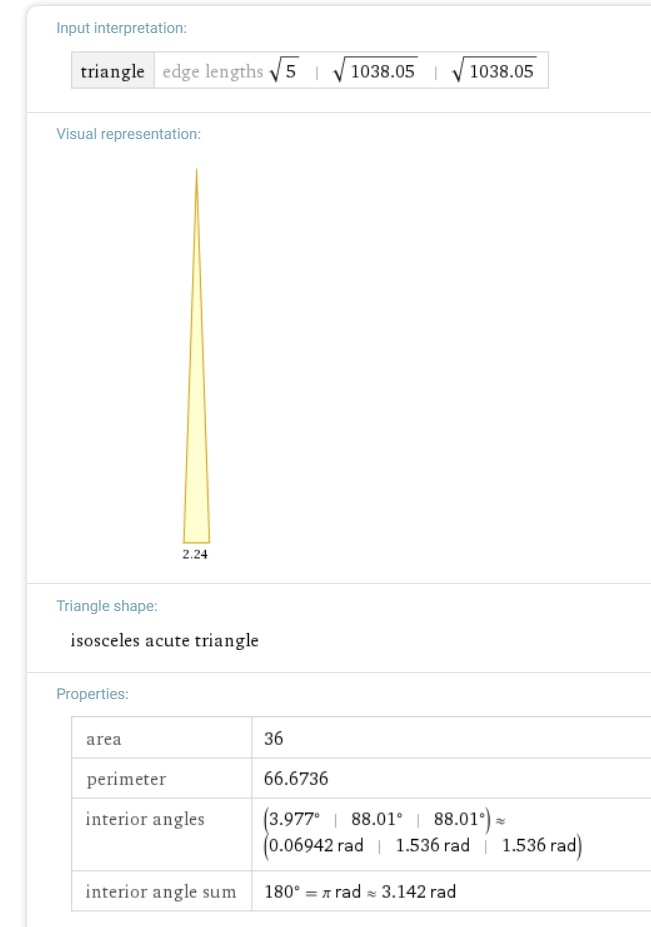
#C (-24.3, 21.4)# side lengths
#AC = sqrt{ (5- -24.3)^2 + (8 - 21.4)^2 } = sqrt{1038.05 }#
#BC=sqrt{ (4- -24.3)^2 + (6 - 21.4)^2 } = sqrt{1038.05} #
#C(33.3, -7.4) # side lengths
#AC = sqrt{(5 - 33.3)^2 + (8- -7.4)^2 } = sqrt{ 1038.05 } #
#BC=sqrt{ (4- 33.3)^2 + (6 - -7.4)^2 } = sqrt{ 1038.05 } #
case AB=BC: #A(5,8), B(4,6), C(x,y).#
# 1^2+2^2 = (x-4)^2 + (y-6)^2 = x^2 -8x + y^2 - 12 y + 16 + 36 #
#0 = x^2 - 8x + y^2 - 12y + 47#
That's a pain because the quadratics didn't cancel. Let's meet with
#0 = x^2 - 8x + y^2 - 12y + 47, y=2x + 70 quad # no real solutions
#0 = x^2 - 8x + y^2 - 12y + 47, y=2x - 74 quad # no real solutions
Nothing here.
case AB=AC: #A(5,8), B(4,6), C(x,y).#
#1^2 + 2^2 = (x-5)^2 + (y-8)^2 = x^2 - 10 x + y^2 - 16 x + 89#
#x^2 - 10 x + y^2 - 16 x + 84 = 0#
#x^2 - 10 x + y^2 - 16 x + 84 = 0 y=2x + 70 quad# no solutions
#x^2 - 10 x + y^2 - 16 x + 84 = 0, y=2x - 74 quad# no solutions


