Given Two corners of an isosceles triangle are at #(6,3) and (5,8)#.
Distance between the corners is given by the expression
#d=sqrt((x_2-x_1)^2+(y_2-y_1)^2)#, inserting given values
#d=sqrt((5-6)^2+(8-3)^2)#
#d=sqrt((-1)^2+(5)^2)#
#d=sqrt26#
Now area of triangle is given by
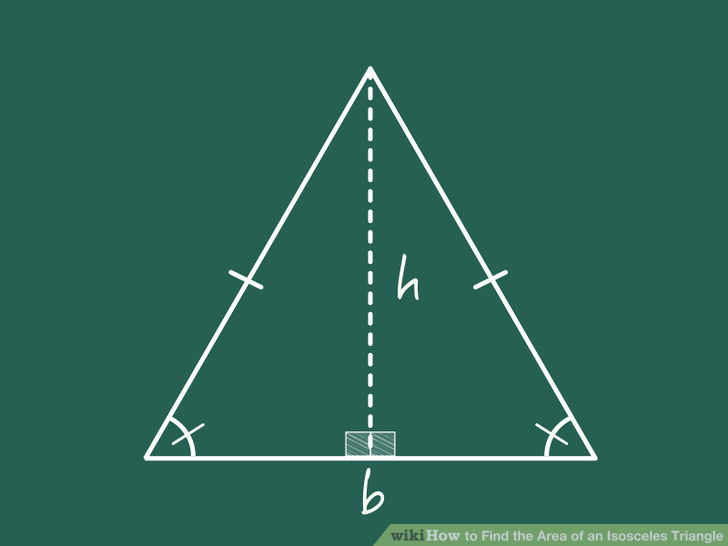
#"Area"=1/2"base"xx"height"#
Case 1. The corners are base angles.
#:."base"=sqrt26#
#"height"=2xx"Area"/"base"# .....(1)
#=2xx8/sqrt26=16/sqrt26#
Now using the Pythagoras theorem
#"leg"=sqrt("height"^2+("base"/2)^2)#
#"leg"=sqrt((16/sqrt26)^2+(sqrt26/2)^2)#
#=sqrt(256/26+26/4#
#=sqrt(128/13+13/2)#
#=sqrt(425/26)#
Case 2. The corners are base angle and the vertex.
#"Leg"=sqrt26#
Let #"base"=b#
Also from (1) #"height"=2xx"Area"/"base"#
#"height"=2xx8/"base"#
#"height"=16/"base"#
Now using the Pythagoras theorem
#"leg"=sqrt("height"^2+("base"/2)^2)#
#sqrt26=sqrt("256/b^2+b^2/4)#, squaring both sides
#26="256/b^2+b^2/4#
#104b^2=1024+b^4#
#b^4-104b^2+1024=0#, solving for #b^2# using the quadratic formula
#b^2=(104+-sqrt((-104)^2-4xx1024xx1))/2#
#b^2=52+-sqrt1680#, taking square root
#b=sqrt(52+-sqrt1680)#, we have ignored the negative sign as length can not be negative.

