Two corners of an isosceles triangle are at (8 ,3 ) and (5 ,4 ). If the triangle's area is 15 , what are the lengths of the triangle's sides?
1 Answer
Explanation:
The length of the given side is
From the formula of the triangle's area:
Since the figure is an isosceles triangle we could have Case 1 , where the base is the singular side, ilustrated by Fig. (a) below
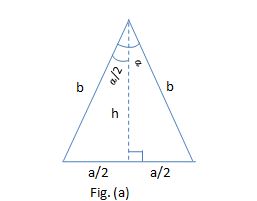 I created this figure using MS Excel
I created this figure using MS Excel
Or we could have Case 2 , where the base is one of the equal sides, ilustrated by Figs. (b) and (c) below
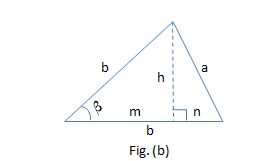 I created this figure using MS Excel
I created this figure using MS Excel
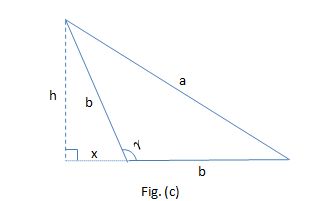 I created this figure using MS Excel
I created this figure using MS Excel
For this problem Case 1 always applies, because:
tan(alpha/2)=(a/2)/h =>h=(1/2)a/tan(alpha/2)
But there's a condition so that Case 2 applies:
sin(beta)=h/b =>h=bsin beta
Orh=bsin gamma
Since the highest value ofsin beta orsin gamma is1 , the highest value ofh , in Case 2, must beb .
In the present problem h is longer than the side to which it is perpendicular, so for this problem only the Case 1 applies.
Solution considering Case 1 (Fig. (a))
b^2=h^2+(a/2)^2
b^2=(30/sqrt(10))^2+(sqrt(10)/2)^2
b^2=900/10+10/4=(900+25)/10=925/10 =>b=sqrt(92.5)=5sqrt(3.7)~=9.618

