First, we need to find the length of the line segment making up the base of the isosceles triangle. The formula for calculating the distance between two points is:
#d = sqrt((color(red)(x_2) - color(blue)(x_1))^2 + (color(red)(y_2) - color(blue)(y_1))^2)#
Substituting the values from the points in the problem gives:
#d = sqrt((color(red)(5) - color(blue)(8))^2 + (color(red)(9) - color(blue)(3))^2)#
#d = sqrt((-3)^2 + 6^2)#
#d = sqrt(9 + 36)#
#d = sqrt(45)#
#d = sqrt(9 * 5)#
#d = sqrt(9)sqrt(5)#
#d = 3sqrt(5)#
he formula for area of a triangle is:
#A= (bh_b)/2#
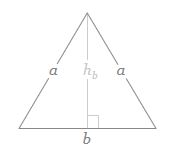
Substituting the Area from the problem and the length of the base we calculated and solving for #h_b# gives:
#4= (3sqrt(5)h_b)/2#
#2/(3sqrt(5)) xx 4= 2/(3sqrt(5)) xx (3sqrt(5)h_b)/2#
#8/(3sqrt(5)) = cancel(2/(3sqrt(5))) xx cancel((3sqrt(5))/2)h_b#
#h_b = 8/(3sqrt(5))#
From an isosceles triangle we know the base and #h_b# are at right angles. Therefore we can use the Pythagorean Theorem to find the length of the sides.
#c^2 = a^2 + b^2#
#c# is what we are solving for.
#a# is the side of the triangle made up of #1/2# the base or:
#1/2 xx 3sqrt(5) = (3sqrt(5))/2#
#b# is #h_b = 8/(3sqrt(5))#
Substituting and solving for #c# gives:
#c^2 = ((3sqrt(5))/2)^2 + (8/(3sqrt(5)))^2#
#c^2 = (9 * 5)/4 + 64/(9 * 5)#
#c^2 = 45/4 + 64/45#
#c^2 = (45/45 xx 45/4) + (4/4 xx 64/45)#
#c^2 = 2025/180 + 256/180#
#c^2 = 2281/180#
#sqrt(c^2) = sqrt(2281/180)#
#c = sqrt(2281)/sqrt(180)#
#c = sqrt(2281)/sqrt(36 * 5)#
#c = sqrt(2281)/(sqrt(36)sqrt(5))#
#c = sqrt(2281)/(6sqrt(5))#

