Name the points #M(8,5) and N(1,7)#
By Distance formula,
#MN=sqrt((1-8)^2+(7-5)^2)=sqrt53#
Given Area #A=15#,
#MN# can be either one of the equal sides or the base of the isosceles triangle.
Case 1) : #MN# is one of the equal sides of the isosceles triangle.
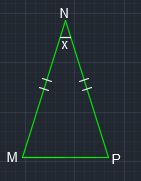
#A=1/2a^2sinx#,
where #a# is one of the equal sides and #x# is the included angle between the two equal sides.
#=> 15=1/2sqrt53^2sinx#
#=> x=sin^-1((2*15)/sqrt53^2)=34.4774^@#
#=> MP# (the base) #= 2*MN*sin(x/2)#
#=2*sqrt53*sin(34.4774/2)=4.31#
Therefore, lengths of the triangle sides are : #sqrt53, sqrt53, 4.31#
Case 2) : MN is the base of the isosceles triangle.
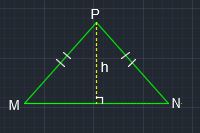
#A=1/2bh#, where #b and h# are the base and the height of the triangle, respectively.
#=> 15=1/2*MN*h#
#=> h=(2*15)/sqrt53=30/sqrt53#
#=> MP=PN# (the equal side) #= sqrt(((MN)/2)^2+h^2)#
#= sqrt((sqrt53/2)^2+(30/sqrt53)^2)#
#=sqrt(6409/212)#
Therefore, lengths of the triangle's sides are #sqrt(6409/212), sqrt(6409/212), sqrt53#
