With the awareness that there may be some exceptions, we can say that the angle between ideal #sp^2# orbitals is #120^@#, due to three coplanar electron groups evenly spanning #360^@#.
One example of when #sp^2# hybridization can occur is when a certain number of electrons need to be donated to other atoms to form a bond, but not all electrons needed are available in the highest-energy orbitals.
Let's say that we wanted to describe the hybridization of one of the carbons in ethene:
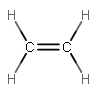
Carbon atom normally has the electron configuration #1s^2 2s^2 2p^2#, so it has four valence electrons, but the #2p# orbitals are a lot higher in energy than hydrogen's #1s# orbital.
To lower the energy of the #2p# orbitals so that they can interact with the #1s# orbital of hydrogen, they can hybridize with the #2s# orbitals to achieve an energy level that is in between those of the pure #2s# and #2p# energy levels.
This allows access to the #2s# electrons.
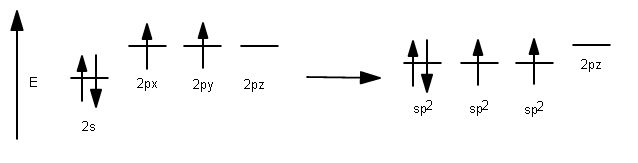
Now, we have three degenerate #\mathbf(sp^2)# hybridized orbitals, formed from one #2s# and two #2p# atomic orbitals (hence #sp^2#).
Although the resultant energy is technically closer to that of the pure #2p# than the pure #2s#, this particular energy level is nevertheless low enough that hybridized bonding becomes favorable, and carbon can now bond with hydrogen with the electrons that originally belonged to the pure #2s# orbital. (And carbon can double bond with another carbon to finish its octet.)
We should also notice that there are 3 electron groups surrounding the #sp^2# carbon. Additionally, the #sp^2# carbon is planar due to the rigid sidelong #\mathbf(p)# orbital overlap of the two carbons.
Therefore, to distribute the atoms evenly in space, while also keeping the planar structure, the angle should be close to or precisely #120^@#.

